题目内容
16. 如图一架云梯AB斜靠在一面墙上,梯子的底端B离墙根O的距离OB长为7米,梯子的顶端A到地面的距离OA为24米.
如图一架云梯AB斜靠在一面墙上,梯子的底端B离墙根O的距离OB长为7米,梯子的顶端A到地面的距离OA为24米.(1)求这个梯子AB的长;
(2)如果梯子的顶端A下滑4米到A′点,梯子的底端B向右滑动到B′点,试求BB′的长.
分析 (1)在△RtAOB中依据勾股定理可知AB2=OA2-OB2=242+72=625,两边同时开方即可求得AB的长;
(2)在Rt△A′OB′中依据勾股定理可求得OB′的长,从而可求得BB′的长.
解答 解:(1)在Rt△AOB中,
∵OA=24,OB=7,
由勾股定理得:AB2=OA2-OB2=242+72=625=252,
∴AB=25;
(2)∵OA′=OA-AA′=24-4=20,
在Rt△A′OB′中,
∵A′B′=25,OA′=20,
由勾股定理得:OB′2-OA′2=252-202=225=152,
∴OB′=15,
∴BB′=OB′-OB=15-7=8.
点评 本题主要考查的是勾股定理的应用,根据梯子的长度不变列出方程是解题的关键.

练习册系列答案
相关题目
1.△ABC是⊙O的内接三角形,⊙O的直径为10,∠ABC=45°,则AC的长是( )
| A. | 5 | B. | 10 | C. | 10$\sqrt{2}$ | D. | 5$\sqrt{2}$ |
8.下列变换不属于全等变换的是( )
| A. | 平移 | B. | 旋转 | C. | 轴对称 | D. | 相似 |
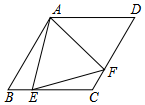 如图,菱形ABCD中,∠B=60°,点E在边BC上,点F在边CD上.若EB=2,DF=3,∠EAF=60°,则△AEF的面积等于$\frac{19\sqrt{3}}{4}$.
如图,菱形ABCD中,∠B=60°,点E在边BC上,点F在边CD上.若EB=2,DF=3,∠EAF=60°,则△AEF的面积等于$\frac{19\sqrt{3}}{4}$.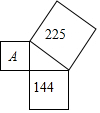 如图,以直角三角形各边向外作正方形,其中两个正方形的面积为225和144,则正方形A的面积为81.
如图,以直角三角形各边向外作正方形,其中两个正方形的面积为225和144,则正方形A的面积为81.