题目内容
11.已知关于x的方程x2-mx+$\frac{m}{2}$-$\frac{1}{4}$=0.(1)求证:无论m取什么数,方程总有两个实数根;
(2)若已知方程有一个实数根是2,试求出另一个实数根.
分析 (1)根据方程的系数结合根的判别式即可得出△=(m-1)2≥0,由此即可证出无论m取什么数,方程总有两个实数根;
(2)将x=2代入原方程可得出关于m的一元一次方程,解之即可得出m的值,设方程的另一根为x0,根据根与系数的关系即可得出关于x0的一元一次方程,解之即可得出方程的另一个实数根.
解答 (1)证明:∵在方程x2-mx+$\frac{m}{2}$-$\frac{1}{4}$=0中,△=(-m)2-4×1×($\frac{m}{2}-\frac{1}{4}$)=m2-2m+1=(m-1)2≥0,
∴无论m取什么数,方程总有两个实数根;
(2)解:将x=2代入原方程得:4-2m+$\frac{m}{2}$-$\frac{1}{4}$=0,
解得:m=$\frac{5}{2}$.
设方程的另一根为x0,
则有:2+x0=m=$\frac{5}{2}$,
∴x0=$\frac{1}{2}$.
∴若已知方程有一个实数根是2,则另一个实数根为$\frac{1}{2}$.
点评 本题考查了根与系数的关系以及根的判别式,解题的关键是:(1)根据根的判别式找出△=(m-1)2≥0;(2)将x=2代入原方程求出m的值.

练习册系列答案
相关题目
2.在下列各图中,不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
6.下列事件是不可能事件的是( )
| A. | 明天是晴天 | B. | 打开电视,正在播放广告 | ||
| C. | 三角形三个内角的和是180° | D. | 两个负数的和是正数 |
20.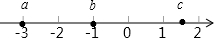 已知有理数a,b,c在数轴上的位置如图所示,则下列说法中不正确的是( )
已知有理数a,b,c在数轴上的位置如图所示,则下列说法中不正确的是( )
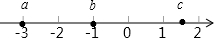 已知有理数a,b,c在数轴上的位置如图所示,则下列说法中不正确的是( )
已知有理数a,b,c在数轴上的位置如图所示,则下列说法中不正确的是( )| A. | a=-3 | B. | b=-1 | C. | a的相反数为正数 | D. | c可能等于2.5 |
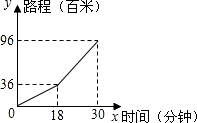 小明早晨从进学校骑车到学校,先上坡后下坡,行程情况如图所示,若返回时上坡、下坡的速度和原来相同,那么小亮从学校骑车回家用的时间是37.2分钟.
小明早晨从进学校骑车到学校,先上坡后下坡,行程情况如图所示,若返回时上坡、下坡的速度和原来相同,那么小亮从学校骑车回家用的时间是37.2分钟. 如图一架云梯AB斜靠在一面墙上,梯子的底端B离墙根O的距离OB长为7米,梯子的顶端A到地面的距离OA为24米.
如图一架云梯AB斜靠在一面墙上,梯子的底端B离墙根O的距离OB长为7米,梯子的顶端A到地面的距离OA为24米.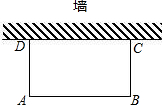 如图,利用一面墙(墙的长度不超过45m),用80m长的篱笆围一个矩形场地,怎样围才能使矩形场地的面积为750m2?
如图,利用一面墙(墙的长度不超过45m),用80m长的篱笆围一个矩形场地,怎样围才能使矩形场地的面积为750m2? 如图,l1∥l2∥l3,AB=3,AD=2,DE=4,EF=7.5,求BC、BF的长.
如图,l1∥l2∥l3,AB=3,AD=2,DE=4,EF=7.5,求BC、BF的长.