题目内容
6.为了节省空间,家里的饭碗一般是摆起来存放的,如果6只饭碗(注:饭碗的大小形状都一样,下同)摆起来的高度为15cm,9只饭碗摆起来的高度为20cm,李老师家的碗橱每格的高度为36cm,则李老师一摞碗最多只能放18只.分析 设碗底的高度为xcm,碗身的高度为ycm,可得碗的高度和碗的个数的关系式为高度=个数×碗底高度+碗身高度,根据6只饭碗摞起来的高度为15cm,9只饭碗摞起来的高度为20cm,列方程组求解,根据碗橱每格的高度为36cm,列不等式求解.
解答 解:设碗底的高度为xcm,碗身的高度为ycm,
由题意得,$\left\{\begin{array}{l}{6x+y=15}\\{9x+y=20}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=\frac{5}{3}}\\{y=5}\end{array}\right.$,
设李老师一摞碗能放a只碗,
$\frac{5}{3}$a+5≤36,
解得:a≤$\frac{93}{5}$,
故李老师一摞碗最多只能放18只碗.
故答案为18.
点评 本题考查了二元一次方程组和一元一次不等式的应用,关键是根据题意,找出合适的等量关系,列方程组和不等式求解.

练习册系列答案
相关题目
7.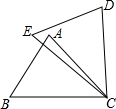 如图,在△ABC和△DEC中,已知BC=EC,∠B=∠E,还需添加一个条件才能使△ABC≌△DEC,不能添加的一个条件是( )
如图,在△ABC和△DEC中,已知BC=EC,∠B=∠E,还需添加一个条件才能使△ABC≌△DEC,不能添加的一个条件是( )
 如图,在△ABC和△DEC中,已知BC=EC,∠B=∠E,还需添加一个条件才能使△ABC≌△DEC,不能添加的一个条件是( )
如图,在△ABC和△DEC中,已知BC=EC,∠B=∠E,还需添加一个条件才能使△ABC≌△DEC,不能添加的一个条件是( )| A. | ∠BCE=∠ACD | B. | AC=DC | C. | ∠A=∠D | D. | AB=DE |
11.为纪念抗日战争胜利70周年,进一步加强爱国主义教育,某校七年级二班决定组织同学们观看爱国主义影片,已知该班$\frac{4}{5}$的学生坐在$\frac{3}{4}$的椅子上,其余的学生因为参加学校组组的合唱团而缺席,若有12张椅子是空着的,请问该班共有多少名学生( )
| A. | 55 | B. | 50 | C. | 45 | D. | 40 |
18.已知△ABC中,∠A=100°,∠B、∠C的平分线的夹角是( )
| A. | 130° | B. | 80° | C. | 140°或40° | D. | 60°或120° |
 如图,在铁路旁边有一李庄,现要建一火车站,为了使李庄人乘火车距离最近,请你在铁路旁选一点来建火车站(位置已选好),说明理由:垂线段最短.
如图,在铁路旁边有一李庄,现要建一火车站,为了使李庄人乘火车距离最近,请你在铁路旁选一点来建火车站(位置已选好),说明理由:垂线段最短.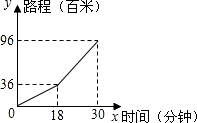 小明早晨从进学校骑车到学校,先上坡后下坡,行程情况如图所示,若返回时上坡、下坡的速度和原来相同,那么小亮从学校骑车回家用的时间是37.2分钟.
小明早晨从进学校骑车到学校,先上坡后下坡,行程情况如图所示,若返回时上坡、下坡的速度和原来相同,那么小亮从学校骑车回家用的时间是37.2分钟. 如图一架云梯AB斜靠在一面墙上,梯子的底端B离墙根O的距离OB长为7米,梯子的顶端A到地面的距离OA为24米.
如图一架云梯AB斜靠在一面墙上,梯子的底端B离墙根O的距离OB长为7米,梯子的顶端A到地面的距离OA为24米.