题目内容
1.△ABC是⊙O的内接三角形,⊙O的直径为10,∠ABC=45°,则AC的长是( )| A. | 5 | B. | 10 | C. | 10$\sqrt{2}$ | D. | 5$\sqrt{2}$ |
分析 首先连接AO,CO,由∠ABC=45°,根据在同圆或等圆中,同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半,即可求得∠AOC的度数,然后利用勾股定理,即可求得弦AC的长.
解答  解:连接AO,CO.
解:连接AO,CO.
∵∠ABC=45°,
∴∠AOC=2∠ABC=90°,
∵⊙O的直径为10,
∴OA=OC=5,
在Rt△AOC中,AC=$\sqrt{O{A}^{2}+O{C}^{2}}$=5$\sqrt{2}$.
故选D.
点评 此题考查了三角形的外接圆与外心,圆周角定理与勾股定理.此题难度适中,准确作出辅助线,求得∠AOC的度数是解此题的关键.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
 如图一架云梯AB斜靠在一面墙上,梯子的底端B离墙根O的距离OB长为7米,梯子的顶端A到地面的距离OA为24米.
如图一架云梯AB斜靠在一面墙上,梯子的底端B离墙根O的距离OB长为7米,梯子的顶端A到地面的距离OA为24米.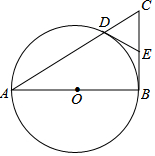 如图,Rt△ABC中,∠ABC=90°,以AB为直径作⊙O交AC于点D,点E为BC的中点,连接DE.
如图,Rt△ABC中,∠ABC=90°,以AB为直径作⊙O交AC于点D,点E为BC的中点,连接DE. 如图,一个点从数轴上的原点开始,先向右移动2个单位长度,再向左移动5个单位长度,可以看到终点表示的数是-3.
如图,一个点从数轴上的原点开始,先向右移动2个单位长度,再向左移动5个单位长度,可以看到终点表示的数是-3. 如图,已知AB=CD,AD=BC,现有下列结论:
如图,已知AB=CD,AD=BC,现有下列结论: 如图,直线a与c的夹角是∠α,直线b与c的夹角是∠β,把直线a“绕”点A按逆时针方向旋转,当∠α与∠β满足∠α+∠β=180°时,直线a∥b,理由是同旁内角互补,两直线平行.
如图,直线a与c的夹角是∠α,直线b与c的夹角是∠β,把直线a“绕”点A按逆时针方向旋转,当∠α与∠β满足∠α+∠β=180°时,直线a∥b,理由是同旁内角互补,两直线平行.