题目内容
12.方程(x3-3x2+4x-3)(x3+2x2-x-1)+5x2-5x+1=0的全部相异实根为( )| A. | 1,-1 | B. | 1,-1,-2 | C. | 1,-1,-2,2 | D. | 以上均不对 |
分析 假设(x3-3x2+4x-3)(x3+2x2-x-1)=(A-B)(A+B),然后分别求出A与B的表达式,进而将原方程化为关于A、B的方程.
解答 解:设(x3-3x2+4x-3)(x3+2x2-x-1)=(A-B)(A+B),
∴$\left\{\begin{array}{l}{A+B={x}^{3}-3{x}^{2}+4x-3}\\{A-B={x}^{3}+2{x}^{2}-x-1}\end{array}\right.$
解得:$\left\{\begin{array}{l}{A={x}^{3}-\frac{{x}^{2}}{2}+\frac{3x}{2}-1}\\{B=-\frac{5{x}^{2}}{2}+\frac{5x}{2}-1}\end{array}\right.$
∴原方程化为:(A+B)(A-B)-2B+1=0,
∴A2-(B-1)2=0
∴(A+B-1)(A-B+1)=0,
∴x3-3x2+4x-4=0或x3+2x2-x-1+1=0,
当x3-3x2+4x-4=0时,
∴(x-2)(x2-x+2)=0,
∴x=2或x2-x+2=0(无解),
当x3+2x2-x-1+1=0时,
∴x(x2+2x-1)=0,
∴x=0或x2+2x-1=0,
∴x=0或x=-1±$\sqrt{2}$
故x=0或x=2或x=-1±$\sqrt{2}$
故选(D)
点评 本题考查高次方程的解法,解题的关键是设(x3-3x2+4x-3)(x3+2x2-x-1)=(A-B)(A+B)进而求出A与B的表示,最后将其转为一元二次方程来进行解答.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
2.在下面各图中,∠1=∠2,能判断AB∥CD的是( )
| A. |  | B. |  | ||
| C. | 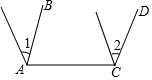 | D. | 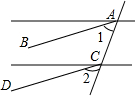 |
7.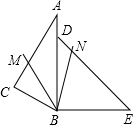 把一副三角尺ABC与BDE按如图所示那样拼在一起,其中A、D、B三点在同一直线上,BM为∠ABC的平分线,BN为∠CBE的平分线,则∠MBN的度数是( )
把一副三角尺ABC与BDE按如图所示那样拼在一起,其中A、D、B三点在同一直线上,BM为∠ABC的平分线,BN为∠CBE的平分线,则∠MBN的度数是( )
 把一副三角尺ABC与BDE按如图所示那样拼在一起,其中A、D、B三点在同一直线上,BM为∠ABC的平分线,BN为∠CBE的平分线,则∠MBN的度数是( )
把一副三角尺ABC与BDE按如图所示那样拼在一起,其中A、D、B三点在同一直线上,BM为∠ABC的平分线,BN为∠CBE的平分线,则∠MBN的度数是( )| A. | 30° | B. | 45° | C. | 55° | D. | 60° |
17.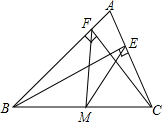 如图,BE、CF是△ABC的高,M是BC的中点,则图中三角形一定是等腰三角形的有( )
如图,BE、CF是△ABC的高,M是BC的中点,则图中三角形一定是等腰三角形的有( )
 如图,BE、CF是△ABC的高,M是BC的中点,则图中三角形一定是等腰三角形的有( )
如图,BE、CF是△ABC的高,M是BC的中点,则图中三角形一定是等腰三角形的有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
4. 如图,扇形的半径为12,圆心角为60°,⊙O为扇形的内切圆,则阴影部分的面积等于( )
如图,扇形的半径为12,圆心角为60°,⊙O为扇形的内切圆,则阴影部分的面积等于( )
 如图,扇形的半径为12,圆心角为60°,⊙O为扇形的内切圆,则阴影部分的面积等于( )
如图,扇形的半径为12,圆心角为60°,⊙O为扇形的内切圆,则阴影部分的面积等于( )| A. | 8 | B. | 8π | C. | 20 | D. | 20π |
1.下列说法中,
①平分弦的直径垂直于弦;
②直径是最长的弦;
③两个三角形全等,那么它们关于一点成中心对称;
④长度相等的弧是等弧;
⑤x2-5x+7=0两根之和为5.
其中正确命题的个数为( )
①平分弦的直径垂直于弦;
②直径是最长的弦;
③两个三角形全等,那么它们关于一点成中心对称;
④长度相等的弧是等弧;
⑤x2-5x+7=0两根之和为5.
其中正确命题的个数为( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
2.若关于x的不等式3x-a≤0的正整数解是1、2、3,则a应满足的条件是( )
| A. | a=9 | B. | a≤9 | C. | 9<a≤12 | D. | 9≤a<12 |
 已知,y=-$\frac{4}{3}$x+4与x轴,y轴的交点分别是点A,B,点C(-2,3),O是原点,求点C到直线AB的距离.
已知,y=-$\frac{4}{3}$x+4与x轴,y轴的交点分别是点A,B,点C(-2,3),O是原点,求点C到直线AB的距离. 如图,已知△ABC,请用尺规作△ABC的中位线EF,使EF∥BC.
如图,已知△ABC,请用尺规作△ABC的中位线EF,使EF∥BC.