题目内容
17.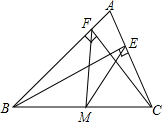 如图,BE、CF是△ABC的高,M是BC的中点,则图中三角形一定是等腰三角形的有( )
如图,BE、CF是△ABC的高,M是BC的中点,则图中三角形一定是等腰三角形的有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
分析 根据直角三角形斜边上的中线等于斜边的一半可得ME=BM=CM,然后根据等腰三角形的定义判断出△BME、△CME是等腰三角形,同理可得△BMF、△CMF是等腰三角形,从而得解.
解答 解:∵BE是△ABC的高,
∴BE⊥CE.
又∵点M是BC的中点,
∴在Rt△BCE中,
ME=BM=CM(直角三角形斜边上的中线等于斜边的一半),
∴△BME、△CME是等腰三角形;
同理,△BMF、△CMF是等腰三角形.
综上所述,△BME、△CME、△BMF、△CMF共4个等腰三角形.
故选C.
点评 本题考查了直角三角形斜边上的中线等于斜边的一半的性质,等腰三角形的判定,熟记性质以及概念并准确识图是解题的关键.

练习册系列答案
相关题目
5.若-xmyn+4与5x2y是同类项,则nm的值为( )
| A. | -9 | B. | 6 | C. | 9 | D. | 16 |
12.方程(x3-3x2+4x-3)(x3+2x2-x-1)+5x2-5x+1=0的全部相异实根为( )
| A. | 1,-1 | B. | 1,-1,-2 | C. | 1,-1,-2,2 | D. | 以上均不对 |
9.下列计算结果为负值的是( )
| A. | (-3)÷(-2) | B. | 0×(-7) | C. | 1-9 | D. | -7-(-10) |
7.下列哪种统计图(表)最不适合用来表示某校男、女学生的人数( )
| A. | 扇形统计图 | B. | 条形统计图 | C. | 折线统计图 | D. | 数据统计表 |

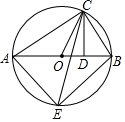 如图,Rt△ABC内接于⊙O,∠ACB=90°,CD⊥AB于点D,CE平分∠OCD.
如图,Rt△ABC内接于⊙O,∠ACB=90°,CD⊥AB于点D,CE平分∠OCD.