题目内容

19．先把二次函数y=x2-2x+3化为y=（x-h）2+k的形式，再解答下列问题：
（1）直接写出相应抛物线的对称轴和顶点坐标；
（2）求出它的图象与坐标轴的交点坐标．

分析 （1）运用配方法把一般式化为顶点式，根据二次函数的性质解答；
（2）根据坐标轴上点的坐标特征，解方程即可．

解答 解：（1）y=x2-2x+3
=（x-1）2+2，
抛物线的对称轴是x=1，顶点坐标（1，2）；
（2）x=0时，y=3，
则抛物线与y轴的交点（0，3），
x2-2x+3=0，
△=4-12＜0，
则抛物线与x轴没有交点．

点评 本题考查的是二次函数的三种形式，正确运用配方法把一般式化为顶点式是解题的关键，注意二次函数的性质的应用．

练习册系列答案
相关题目
9．已知二次函数y=-（x-1）2+4．
（1）求出二次函数的顶点坐标及与x轴交点坐标，在网格中画出草图．
（2）观察图象确定：x取何值时，y＞0．
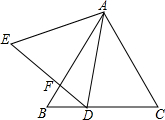10．如图，正△ABC的边长为6，点D是BC边上一点，连结AD，将AD绕点A顺时针旋转60°得AE，连结DE交AB于点F．
（1）填空：若∠BAD=20°，则∠BDF=40°；
（2）若当点D在线段BC上运动时（不与B、C两点重合），设BD=x，BF=y，
试求y与x之间的函数关系式；
（3）若$\frac{BD}{DC}$=$\frac{1}{2}$，请求出AE的长．
7．有下列二次函数：
①y=-x2+2；②y=2x2-4x+2；③y=x2；④y=-x2+2x+3；⑤$y=\frac{1}{2}{x^2}-7$；⑥$y=-\frac{1}{2}{x^2}+x-\frac{1}{2}$．
其图象的顶点在y轴上的个数为（　　）
A．2个B．3个C．4个D．5个
14．已知关于x的方程kx2-2x+3=0有两个不相等的实数根x1、x2．
（1）求k的取值范围；
（2）k为何值时，方程的两根满足x1=3x2？
4．已知（-2x2）（3x2-ax-b）-3x3+x2中不含x的二次项和三次项，则a+b=1．
11．将长方形ABCD按如图所示沿EF所在直线折叠，点C落在AD上的点C′处，点D落在点D′处．
（1）求证：△EFC′是等腰三角形．
（2）如果∠1=65°，求∠2的度数．
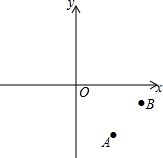8．如图，已知平面直角坐标系，A，B两点的坐标分别为A（4，-6），B（8，-2）．
（1）若P（0，p）是y轴上的一个动点，则当p=-$\frac{14}{3}$时，△PAB的周长最短；
（2）若C（0，b），D（0，b+6）是y轴上的两个动点，则当b=-$\frac{20}{3}$时，四边形ABDC的周长最短；
（3）设M，N分别为x轴和y轴上的动点，请问：是否存在这样的点M（m，0），N（0，n），使四边形ABMN的周长最短？若存在，请求出m=5，n=-$\frac{10}{3}$，（不必写解答过程）；若不存在，请说明理由．
9．下列是勾股数的是（　　）
A．7，8，9B．5，7，12C．13，15，17D．21，28，35

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网