题目内容
10.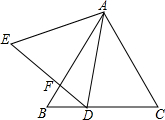 如图,正△ABC的边长为6,点D是BC边上一点,连结AD,将AD绕点A顺时针旋转60°得AE,连结DE交AB于点F.
如图,正△ABC的边长为6,点D是BC边上一点,连结AD,将AD绕点A顺时针旋转60°得AE,连结DE交AB于点F.(1)填空:若∠BAD=20°,则∠BDF=40°;
(2)若当点D在线段BC上运动时(不与B、C两点重合),设BD=x,BF=y,
试求y与x之间的函数关系式;
(3)若$\frac{BD}{DC}$=$\frac{1}{2}$,请求出AE的长.
分析 (1)先证△AED是等边三角形,从而∠BDF=∠EAF;
(2)证明△BDF∽△CAD,列出相似比例关系即可;
(3)过点D作DG⊥AC于G,求出DG、AG,就可求出AD,而AD=AE.
解答 解:(1)∵AE=AD,∠DAE=60°,
∴△AED是等边三角形,
∴∠AED=∠ADE=60°,
∵∠ABC=60°,
∴∠BDF=∠EAF,
∵∠BAD=20°,
∴∠EAF=40°,
∴∠BDF=40°;
(2)∵∠EDA=60°,
∴∠BDF+∠ADC=120°,
∵∠ACB=60°,
∴∠ADC+∠DAC=120°,
∴∠BDF=∠DAC,
∴△BDF∽△CAD,
∴$\frac{BF}{BD}=\frac{CD}{AC}$,
∵BF=y,BD=x,AB=BC=AC=6,
∴$\frac{y}{x}=\frac{6-x}{6}$,
∴$y=-\frac{1}{6}{x}^{2}+x$;
(3)过点D作DG⊥AC于G,如图,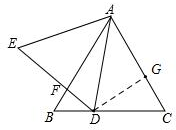
∵BC=6,$\frac{BD}{CD}=\frac{1}{2}$,
∴BD=2,CD=4,
∵∠ACB=60°,
∴CG=2,DG=2$\sqrt{3}$,
∴AG=4,
∴AD=$2\sqrt{7}$,
∵△AED是等边三角形,
∴AE=AD=$2\sqrt{7}$.
点评 本题考查了等边三角形的性质、旋转的性质、三角形内角和定理、相似三角形的判定与性质、特殊角的三角函数、勾股定理等知识点,难度中等.第(1)问的关键是转移角度;知道“一线三等角相似模型”是迅速解决第(2)问的关键;对于线段长度的求法,往往构造直角三角形,利用勾股定理解决.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.$\frac{{\sqrt{x+1}}}{{\sqrt{x}}}$有意义的条件是( )
| A. | x≥-1 | B. | x>0 | C. | x>-1 | D. | x≥0 |
5. 如图,△ABC≌△EFD,AB∥EF,DF∥BC,则∠B的对应角是( )
如图,△ABC≌△EFD,AB∥EF,DF∥BC,则∠B的对应角是( )
 如图,△ABC≌△EFD,AB∥EF,DF∥BC,则∠B的对应角是( )
如图,△ABC≌△EFD,AB∥EF,DF∥BC,则∠B的对应角是( )| A. | ∠F | B. | ∠FDE | C. | ∠E | D. | 以上都不正确 |
15.将抛物线y=x2+2向右平移3个单位后所得抛物线的解析式为( )
| A. | y=(x-3)2+2 | B. | y=x2+5 | C. | y=(x+3)2+2 | D. | y=x2-1 |
2.下列方程中,是关于x的一元二次方程为( )
| A. | 3x+1=5x+7 | B. | $\frac{1}{{x}^{2}}$+x-1=0 | ||
| C. | x2-5=0 | D. | ax2-bx=5(a和b为常数) |
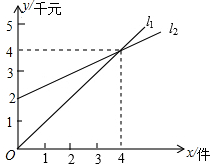 如图,l1、l2分别表示某种产品的销售收入与销售件数的函数关系图象和销售成本与件数的函数关系图象.
如图,l1、l2分别表示某种产品的销售收入与销售件数的函数关系图象和销售成本与件数的函数关系图象. 如图:在△ABC中,BF=CF,BD⊥AC于D,CE⊥AB于E,BD、CE相交于F.
如图:在△ABC中,BF=CF,BD⊥AC于D,CE⊥AB于E,BD、CE相交于F.