题目内容
4．已知（-2x2）（3x2-ax-b）-3x3+x2中不含x的二次项和三次项，则a+b=1．分析 根据单项式乘多项式的法则计算并合并同类项，再根据含x的二次项和三次项的系数为0列式计算即可．
解答 解：（-2x2）•（3x2-ax-b）-3x3+x2=-6x4+（2a-3）x3+（2b+1）x2，
∵不含x的二次项和三次项，
∴2a-3=0，2b+1=0，
∴a=$\frac{3}{2}$，b=-$\frac{1}{2}$，
a+b=1．
故答案为：1．
点评 本题主要考查了多项式乘多项式的运算，注意当要求多项式中不含有哪一项时，应让这一项的系数为0．
练习册系列答案
一本好题口算题卡系列答案
相关题目
14．
小敏从A地出发向B地行走，同时小聪从B地出发向A地行走，如图所示，相交于点P的两条线段l1、l2分别表示小敏、小聪离B地的距离ykm与已用时间xh之间的关系，则小敏、小聪行走的速度分别是（ ）
小敏从A地出发向B地行走，同时小聪从B地出发向A地行走，如图所示，相交于点P的两条线段l1、l2分别表示小敏、小聪离B地的距离ykm与已用时间xh之间的关系，则小敏、小聪行走的速度分别是（ ）| A． | 3km/h和4km/h | B． | 3km/h和3km/h | C． | 4km/h和4km/h | D． | 4km/h和3km/h |
15．将抛物线y=x2+2向右平移3个单位后所得抛物线的解析式为（ ）
| A． | y=（x-3）2+2 | B． | y=x2+5 | C． | y=（x+3）2+2 | D． | y=x2-1 |
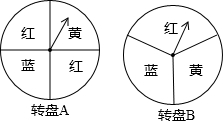小明和小芳做一个“配色”的游戏，下图是两个可以自由转动的转盘，每个转盘被分成面积相等的几个扇形，并涂上图中所示的颜色．同时转动两个转盘，如果转盘A转出了红色，转盘B转出了蓝色，或者转盘A转出了蓝色，转盘B转出了红色，则红色和蓝色在一起配成紫色，这种情况下小芳获胜；同样，蓝色和黄色在一起配成绿色，这种情况下小明获胜；在其它情况下，则小明、小芳不分胜负．
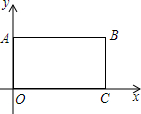如图，在平面直角坐标系中，矩形OABC四个顶点的坐标分别为O（0，0），A（0，3），B（6，3），C（6，0），抛物线过y=ax2+bx+c（a≠0）点A．