题目内容
11. 将长方形ABCD按如图所示沿EF所在直线折叠,点C落在AD上的点C′处,点D落在点D′处.
将长方形ABCD按如图所示沿EF所在直线折叠,点C落在AD上的点C′处,点D落在点D′处.(1)求证:△EFC′是等腰三角形.
(2)如果∠1=65°,求∠2的度数.
分析 (1)根据折叠的性质得到∠EFC′=∠1,由平行线的性质得到∠1=∠FBC′,等量代换得到∠EFC′=′FEC′,根据等腰三角形的判定定理即可得到结论;
(2)根据折叠的性质和已知条件得到∠EC′F=180°-∠FEC′-∠EFC′=180°-65°=65°=50°,由于∠D′C′F=∠2+∠EC′F=∠C=90°即可得到结论.
解答 (1)证明:四边形EFC′D′是将长方形ABCD中的四边形CDEF沿EF所在直线折叠得到的,
∴∠EFC′=∠1,
∵AD∥BC,
∴∠1=∠FBC′,
∴∠EFC′=′FEC′,
∴FC′=EC′,
∴△EFC′是等腰三角形;
(2)解:∵∠1=∠FEC′=∠EFC′,∠1=65°,
∴∠EC′F=180°-∠FEC′-∠EFC′=180°-65°=65°=50°,
∵∠D′C′F=∠2+∠EC′F=∠C=90°,
∴∠2=90°-∠EC′F=40°,
∴∠2=50°.
点评 本题考查了翻折变换-折叠问题,矩形的性质,平行线的性质,等腰三角形的判定,熟练掌握折叠的性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.下列方程中,是关于x的一元二次方程为( )
| A. | 3x+1=5x+7 | B. | $\frac{1}{{x}^{2}}$+x-1=0 | ||
| C. | x2-5=0 | D. | ax2-bx=5(a和b为常数) |
6.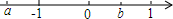 已知a,b在数轴上的位置如图所示,则化简|a+b|+$\sqrt{(a-b)^{2}}$的结果为( )
已知a,b在数轴上的位置如图所示,则化简|a+b|+$\sqrt{(a-b)^{2}}$的结果为( )
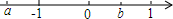 已知a,b在数轴上的位置如图所示,则化简|a+b|+$\sqrt{(a-b)^{2}}$的结果为( )
已知a,b在数轴上的位置如图所示,则化简|a+b|+$\sqrt{(a-b)^{2}}$的结果为( )| A. | -2a | B. | 2b | C. | -2b | D. | 2a |
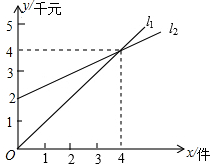 如图,l1、l2分别表示某种产品的销售收入与销售件数的函数关系图象和销售成本与件数的函数关系图象.
如图,l1、l2分别表示某种产品的销售收入与销售件数的函数关系图象和销售成本与件数的函数关系图象.
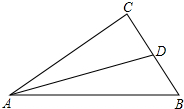 如图,在△ABC中,∠C=90°,AC=BC,AD平分∠BAC,且CD=1,则△ABD的面积为$\frac{2+\sqrt{2}}{2}$.
如图,在△ABC中,∠C=90°,AC=BC,AD平分∠BAC,且CD=1,则△ABD的面积为$\frac{2+\sqrt{2}}{2}$.