题目内容
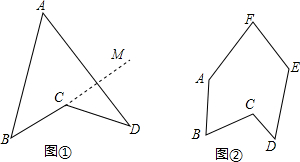
16．
如图，DE是△ABC的中位线，F是DE的中点，CF的延长线交AB于点G，则AG：GD的值为2．
分析 根据三角形中位线定理，推出DF：BC=GD：GB=1：4，推出DG：DB=GD：AD=1：3由此即可解决问题．
解答 解：∵DE是△ABC的中位线，
∴DE=$\frac{1}{2}$BC，DE∥BC，
∵DF=FE，
∴DF=$\frac{1}{4}$BC，
∴$\frac{GD}{GB}$=$\frac{DF}{BC}$=$\frac{1}{4}$，
∴$\frac{GD}{DB}$=$\frac{1}{3}$，
∵AD=BD，
∴GD：AD=1：3，
∴AG：GD=2：1，
故答案为2．
点评 本题考查三角形中位线性质、平行线分线段成比例定理等知识，解题的关键是灵活运用三角形中位线定理，推出GD：GB=DF：BC=1：4这个突破口，属于中考常考题型．
练习册系列答案
相关题目
7．
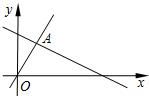如图，函数y=2x和y=ax+4的图象相交于点A（m，3），则m+a的值为（ ）
如图，函数y=2x和y=ax+4的图象相交于点A（m，3），则m+a的值为（ ）| A． | -1 | B． | $\frac{5}{6}$ | C． | 1 | D． | $\frac{13}{6}$ |
1．在平面直角坐标系中，若y轴上的点P到x轴的距离为3，则点P的坐标为（ ）
| A． | （3，0） | B． | （3，0）或（-3，0） | C． | （0，3） | D． | （0，3）或（0，-3） |
8．已知∠AOB=50°，∠BOC=30°，OD平分∠AOC，则∠AOD的度数为（ ）
| A． | 20° | B． | 80° | C． | 10°或40° | D． | 20°或80° |
