题目内容
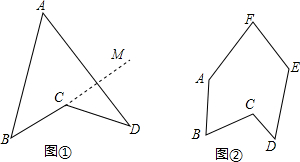
4.把多边形的某些边向两方延长,其他各边若不全在延长所得直线的同侧,则把这样的多边形叫做凹多边形,如图(1)四边形ABCD中,作BC的延长线CM,则边AB、CD分别在直线BM的两侧,所以四边形ABCD就是一个凹四边形,我们来简单研究凹多边形的边和角的性质.(1)请你画一个凹五边形;
(2)如图②,在凹六边形ABCDEF中,探索∠BCD与∠A、∠B、∠D、∠E、∠F之间的关系;
(3)如图①,在凹四边形ABCD中,证明AB+AD>BC+CD.
分析 (1)直接利用凹五边形的定义分析得出答案;
(2)根据题意结合凸多边形的性质得出540°-(180°-∠BCD)=∠A+∠B+∠D+∠E+∠F,进而得出答案;
(3)利用三角形三边关系,再结合不等式的性质进而得出答案.
解答 解:(1)如图1所示:即为凹五边形 ;
;
(2)如图2,
连接BD,
由多边形内角和定理可得:五边形ABDEF的内角和为:540°,△BCD的内角和为:180°,
故540°-(180°-∠BCD)=∠A+∠B+∠D+∠E+∠F,
则360°+∠BCD=∠A+∠B+∠D+∠E+∠F;
(3)如图3,
设DA与直线BC的交点为E,
在△ABE中,BA+AE>BE,
△CED中,EC+ED>CD,
故AB+AE+EC+ED>BE+CD
则AB+AD>BC+CD.
点评 此题主要考查了四边形综合以及凸多边形的性质以及凹多边形与凸多边形的性质等知识,正确将凹多边形与凸多边形的关系是解题关键.

练习册系列答案
相关题目
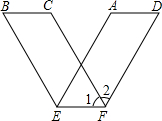 用平行四边形纸条沿对边AB、CD上的点E、F所在的直线折成V字形图案,已知图中∠1=62°,则∠2的度数为56°.
用平行四边形纸条沿对边AB、CD上的点E、F所在的直线折成V字形图案,已知图中∠1=62°,则∠2的度数为56°. 如图,DE是△ABC的中位线,F是DE的中点,CF的延长线交AB于点G,则AG:GD的值为2.
如图,DE是△ABC的中位线,F是DE的中点,CF的延长线交AB于点G,则AG:GD的值为2.