题目内容
5.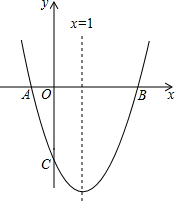 如图,已知抛物线y=ax2+bx+c与x轴交于A,B两点.交y轴与C点,已知抛物线的对称轴为x=1,B(3,0),C(0,-3)
如图,已知抛物线y=ax2+bx+c与x轴交于A,B两点.交y轴与C点,已知抛物线的对称轴为x=1,B(3,0),C(0,-3)(1)求这条抛物线所对应的函数关系式;
(2)在抛物线的对称轴上是否存在一点P,使点P到B,C两点的距离之差最大?若存在,求出点P的坐标;若不存在,请说明理由.
分析 (1)将B、C点的坐标代入抛物线解析式,联立对称轴-$\frac{b}{2a}$=1成方程组,解方程组即可得出结论;
(2)假设存在,连接AC,延长AC交抛物线的对称轴于点P.由三角形内两边之差小于第三边得出当A、C、P三点共线时,点P到B,C两点的距离之差最大,由A、C点坐标利用待定系数法即可求出直线AC的解析式,令x=1,求出y值即可得出P点的坐标.
解答 解:(1)由已知得:$\left\{\begin{array}{l}{-\frac{b}{2a}=1}\\{0=9a+3b+c}\\{-3=c}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=1}\\{b=-2}\\{c=-3}\end{array}\right.$.
∴这条抛物线所对应的函数关系式为y=x2-2x-3.
(2)假设存在,连接AC,延长AC交抛物线的对称轴于点P,如图所示.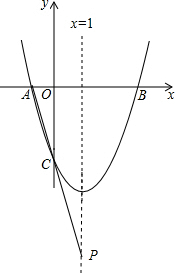
令y=0,则有x2-2x-3=0,
解得:x=-1,或x=3.
即点A的坐标为(-1,0).
在对称轴x=1上任取一定不同于点P的点P′.
由抛物线的对称性可知:P′B=P′A,PB=PA,
P′B-P′C=P′A-P′C<AC=PA-PC=PB-PC,
∴当A、C、P三点共线时,点P到B,C两点的距离之差最大.
设直线AC的解析式为y=kx-3,
∵点A(-1,0)在直线AC上,
∴有-k-3=0,解得:k=-3,
即直线AC的解析式为y=-3x-3.
令x=1,则y=-3×1-3=-6,
点P的坐标为(1,-6).
故在抛物线的对称轴上存在一点P,使点P到B,C两点的距离之差最大,点P的坐标为(1,-6).
点评 本题考查了待定系数法求函数解析式、抛物线与x轴的交点以及三角形三边关系,解题的关键是:(1)利用待定系数法求函数解析式;(2)找出P点的位置.本题属于基础题,难度不大,解决该题型题目时,由三角形三边关系“三角形内两边之差小于第三边”判断P点的位置是关键.

 中考解读考点精练系列答案
中考解读考点精练系列答案| A. | -$\sqrt{5}$ | B. | 0 | C. | $\frac{1}{3}$ | D. | 6 |
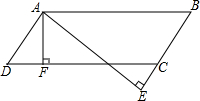 如图,过?ABCD的顶点A分别作AF⊥DC于F,AE⊥BC交BC的延长线于点E,若AE=3.5cm,AF=2.8cm,∠EAF=30°,则AB=7cm,AD=5.6cm.
如图,过?ABCD的顶点A分别作AF⊥DC于F,AE⊥BC交BC的延长线于点E,若AE=3.5cm,AF=2.8cm,∠EAF=30°,则AB=7cm,AD=5.6cm.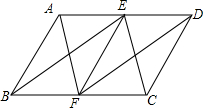 如图,在?ABCD中,E,F分别为AD,BC的中点,连接EF,AF,BE,CE,DF,则图中和四边形ABFE面积相等的四边形有( )个.
如图,在?ABCD中,E,F分别为AD,BC的中点,连接EF,AF,BE,CE,DF,则图中和四边形ABFE面积相等的四边形有( )个. 如图,在?ABCD中,∠ABC的平分线交AD于E,∠BED=150°,则∠A的度数为120°.
如图,在?ABCD中,∠ABC的平分线交AD于E,∠BED=150°,则∠A的度数为120°.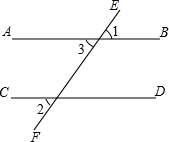 (1)如图,已知直线EF与AB、CD都相交,AB∥CD.
(1)如图,已知直线EF与AB、CD都相交,AB∥CD.