题目内容
10．
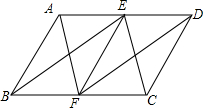如图，在?ABCD中，E，F分别为AD，BC的中点，连接EF，AF，BE，CE，DF，则图中和四边形ABFE面积相等的四边形有（ ）个．| A． | 1 | B． | 2 | C． | 3 | D． | 5 |
分析 由平行四边形的性质和已知条件周长四边形ABFE、四边形EFCD，四边形AFCE、四边形BFDE是平行四边形，得出四边形ABFE的面积=四边形EFCD的面积=四边形AFCE的面积=四边形BFDE的面积=$\frac{1}{2}$?ABCD的面积，即可得出结论．
解答 解：∵四边形ABCD是平行四边形，
∴AD=BC，AD∥BC，
∵E，F分别为AD，BC的中点，
∴AE=DE=BF=CF，
∴四边形ABFE、四边形EFCD，四边形AFCE、四边形BFDE是平行四边形，
∴四边形ABFE的面积=四边形EFCD的面积=四边形AFCE的面积=四边形BFDE的面积=$\frac{1}{2}$?ABCD的面积，
∴图中和四边形ABFE面积相等的四边形有3个，
故选：C．
点评 本题考查了平行四边形的性质与判定；熟练掌握平行四边形的性质，证明四边形ABFE、四边形EFCD，四边形AFCE、四边形BFDE是平行四边形是解决问题的关键．
练习册系列答案
王后雄学案教材完全解读系列答案
海淀课时新作业金榜卷系列答案
相关题目
B. 
C. 
D. 
1．
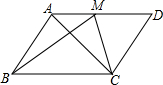如图所示，?ABCD中，M为AD的中点，BM平分∠ABC，则（ ）
如图所示，?ABCD中，M为AD的中点，BM平分∠ABC，则（ ）| A． | CM可能垂直于AD | B． | AC不可能垂直于CD | ||
| C． | CM不可能垂直于AD | D． | CM可能平分∠ACD |
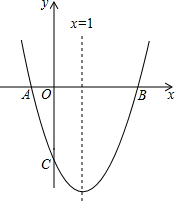如图，已知抛物线y=ax2+bx+c与x轴交于A，B两点．交y轴与C点，已知抛物线的对称轴为x=1，B（3，0），C（0，-3）
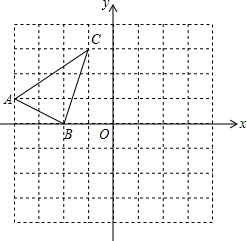（1）请你把△ABC平移到△DEF，使点A（-4，1）的对应点D的坐标为（1，-2），B、C的对应点分别为E、F．
如图，在?ABCD中，O为BD的中点，过O作两条互相垂直的直线，分别交四边形ABCD于E，F，G，H，求证：四边形EFGH是菱形．