题目内容
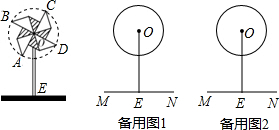
如图,风车的支杆OE垂直于桌面,风车中心O到桌面的距离OE为25cm,小小风车在风吹动下绕着中心O不停地转动,转动过程中,叶片端点A、B、C、D在同一圆O上,已知⊙O的半径为10cm.
(1)风车在转动过程中,点A到桌面的最远距离为 cm,最近距离为 cm.
(2)风车在转动过程中,当∠AOE=45°时,求点A到桌面的距离(结果保留根号).
(3)在风车转动一周的过程中,求点A相对于桌面的高度不超过20cm所经过的路径长(结果保留π).
(1)风车在转动过程中,点A到桌面的最远距离为
(2)风车在转动过程中,当∠AOE=45°时,求点A到桌面的距离(结果保留根号).
(3)在风车转动一周的过程中,求点A相对于桌面的高度不超过20cm所经过的路径长(结果保留π).

考点:圆的综合题
专题:综合题
分析:(1)点A到最上面时到桌面的距离最远,在最下面时,距离桌面最近;
(2)作A1F⊥MN于点F,A1G⊥OE于点G,在Rt△A1OG中,利用三角函数可求得OG,从而得出点A到桌面的距离A1F;
(3)作A2H⊥MN于H,则A2H=20.作A2D⊥OE于点D,则DE=A2H.在Rt△A2OD中,由特殊角的三角函数得∠A2OD=60°,由圆的轴对称性可知,∠A3OA2=2∠A2OD=120°.从而得出点A所经过的路径长.
(2)作A1F⊥MN于点F,A1G⊥OE于点G,在Rt△A1OG中,利用三角函数可求得OG,从而得出点A到桌面的距离A1F;
(3)作A2H⊥MN于H,则A2H=20.作A2D⊥OE于点D,则DE=A2H.在Rt△A2OD中,由特殊角的三角函数得∠A2OD=60°,由圆的轴对称性可知,∠A3OA2=2∠A2OD=120°.从而得出点A所经过的路径长.
解答: 解:(1)点A到最上面时到桌面的距离最远,此时最远距离=OE+OA=35cm,
解:(1)点A到最上面时到桌面的距离最远,此时最远距离=OE+OA=35cm,
点A到最下面时到桌面的距离最近,此时最近距离=OE-OA=15cm,
(2)如图1,点A运动到点A1的位置时∠AOE=45°,
作A1F⊥MN于点F,A1G⊥OE于点G,
∴A1F=GE,
在Rt△A1OG中,
∵∠A1OG=45°,OA1=10,
∴OG=OA1•cos45°=10×
=5
,
∵OE=25,
∴GE=OE-OG=25-5
,
∴A1F=GE=25-5
,
∴点A到桌面的距离是(25-5
)厘米.
(3)如图2,点A在旋转过程中运动到点A2、A3的位置时,点A到桌面的距离等于20厘米.
作A2H⊥MN于H,则A2H=20,
作A2D⊥OE于点D,
∴DE=A2H,
∵OE=25,
∴OD=OE-DE=25-20=5.
在Rt△A2OD中,
∵OA2=10,
∴cos∠A2OD=
=
=
.
∴∠A2OD=60°,
由圆的轴对称性可知,∠A3OA2=2∠A2OD=120°,
∴点A所经过的路径长为
=
.
 解:(1)点A到最上面时到桌面的距离最远,此时最远距离=OE+OA=35cm,
解:(1)点A到最上面时到桌面的距离最远,此时最远距离=OE+OA=35cm,点A到最下面时到桌面的距离最近,此时最近距离=OE-OA=15cm,
(2)如图1,点A运动到点A1的位置时∠AOE=45°,
作A1F⊥MN于点F,A1G⊥OE于点G,
∴A1F=GE,
在Rt△A1OG中,
∵∠A1OG=45°,OA1=10,
∴OG=OA1•cos45°=10×
| ||
| 2 |
| 2 |
∵OE=25,
∴GE=OE-OG=25-5
| 2 |
∴A1F=GE=25-5
| 2 |
∴点A到桌面的距离是(25-5
| 2 |
(3)如图2,点A在旋转过程中运动到点A2、A3的位置时,点A到桌面的距离等于20厘米.

作A2H⊥MN于H,则A2H=20,
作A2D⊥OE于点D,
∴DE=A2H,
∵OE=25,
∴OD=OE-DE=25-20=5.
在Rt△A2OD中,
∵OA2=10,
∴cos∠A2OD=
| OD |
| OA2 |
| 5 |
| 10 |
| 1 |
| 2 |
∴∠A2OD=60°,
由圆的轴对称性可知,∠A3OA2=2∠A2OD=120°,
∴点A所经过的路径长为
| 120π×10 |
| 180 |
| 20π |
| 3 |
点评:本题考查了圆的综合,解答本题的关键是作出辅助线,涉及了解直角三角形、锐角三角函数的定义,解答本题的关键是数形结合思想的运用,有一定难度.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
 如图,已知E、F是矩形ABCD对角线AC上的两点,且BE⊥AC,DF⊥AC.
如图,已知E、F是矩形ABCD对角线AC上的两点,且BE⊥AC,DF⊥AC. 如图,四边形ABCD是正方形,△ADE经顺时针旋转后与△ABF重合.
如图,四边形ABCD是正方形,△ADE经顺时针旋转后与△ABF重合. 如图,在△ABC中,∠ACB=90°,AC=6,BC=8,以斜边AB为边向外作正方形ABDE,连接CE,则CE的长是
如图,在△ABC中,∠ACB=90°,AC=6,BC=8,以斜边AB为边向外作正方形ABDE,连接CE,则CE的长是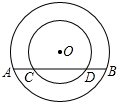 如图,以点O为圆心的两个同心圆,两个圆的半径分别为5cm和9cm,大圆的弦AB交小圆于点C、D且CD=8cm,求AC和BD的长.
如图,以点O为圆心的两个同心圆,两个圆的半径分别为5cm和9cm,大圆的弦AB交小圆于点C、D且CD=8cm,求AC和BD的长.