题目内容
如图，四边形ABCD是正方形，△ADE经顺时针旋转后与△ABF重合．（1）旋转中心是哪一点？
（2）则△ADE绕点A旋转了多少度？
（3）如果连接EF，那么△AEF是怎样的三角形？
考点：旋转的性质
专题：
分析：（1）根据图形判断点A为旋转中心；
（2）根据对应边AB、AD的夹角∠BAD等于旋转角解答；
（3）根据旋转的性质可得AE=AF，∠EAF=90°，然后根据等腰直角三角形的定义判定即可．
（2）根据对应边AB、AD的夹角∠BAD等于旋转角解答；
（3）根据旋转的性质可得AE=AF，∠EAF=90°，然后根据等腰直角三角形的定义判定即可．
解答：解：（1）旋转中心为点A；
（2）∵四边形ABCD是正方形，
∴∠BAD=90°，
∴旋转角为∠BAD=90°；
（3）由旋转的性质得，AE=AF，∠EAF=90°，
所以△AEF是等腰直角三角形．
（2）∵四边形ABCD是正方形，
∴∠BAD=90°，
∴旋转角为∠BAD=90°；
（3）由旋转的性质得，AE=AF，∠EAF=90°，
所以△AEF是等腰直角三角形．
点评：本题考查了旋转的性质，正方形的性质，等腰直角三角形的判定，熟记性质并准确识图是解题的关键．
练习册系列答案
世纪百通期末金卷系列答案
相关题目
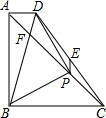等腰Rt△ABC中，∠ABC=90°，且AB=BC，P为AC上一点，以BP为直角边向上作等腰Rt△BPD，∠BPD=90°．