题目内容
 如图,已知E、F是矩形ABCD对角线AC上的两点,且BE⊥AC,DF⊥AC.
如图,已知E、F是矩形ABCD对角线AC上的两点,且BE⊥AC,DF⊥AC.(1)求证:△ABE≌△CDF;
(2)若AE:EF:FC=1:2:1,试求∠ACB的度数.
考点:矩形的性质,全等三角形的判定与性质
专题:
分析:(1)利用矩形的性质得出对应角以及对应线段,再利用全等三角形的判定方法求出即可;
(2)利用相似三角形的判定与性质得出BE=
x,进而利用锐角三角函数关系得出即可.
(2)利用相似三角形的判定与性质得出BE=
| 3 |
解答:(1)证明:∵E、F是矩形ABCD对角线AC上的两点,且BE⊥AC,DF⊥AC,
∴∠AEB=∠DFC=90°,∠BAE=∠DCF,AB=DC,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(AAS);
(2)解:∵∠BAE+∠ABE=90°,∠ABE+∠EBC=90°,
∴∠BAE=∠CBE,
又∵∠AEB=∠BEC,
∴△ABE∽△BCE,
∴
=
,
∵AE:EF:FC=1:2:1,
∴设AE=x,EF=2x,FC=x,
∴
=
,
∴BE=
x,
∴tan∠ECB=
=
=
,
∴∠ECB=30°即∠ACB的度数为30°.
∴∠AEB=∠DFC=90°,∠BAE=∠DCF,AB=DC,
在△ABE和△CDF中,
|
∴△ABE≌△CDF(AAS);
(2)解:∵∠BAE+∠ABE=90°,∠ABE+∠EBC=90°,
∴∠BAE=∠CBE,
又∵∠AEB=∠BEC,
∴△ABE∽△BCE,
∴
| AE |
| BE |
| BE |
| EC |
∵AE:EF:FC=1:2:1,
∴设AE=x,EF=2x,FC=x,
∴
| x |
| BE |
| BE |
| 3x |
∴BE=
| 3 |
∴tan∠ECB=
| BE |
| EC |
| ||
| 3x |
| ||
| 3 |
∴∠ECB=30°即∠ACB的度数为30°.
点评:此题主要考查了全等三角形的判定与性质以及相似三角形的判定与性质以及锐角三角函数关系等知识,表示出BE的长是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
在△ABC中,∠C=90°,若tanB=
,则sinA=( )
| 5 |
| 12 |
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,在正方形网格上有一个△ABC.
如图,在正方形网格上有一个△ABC.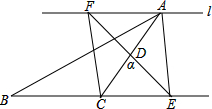 如图,在△ABC中∠ACB=90°,D是AC的中点,过点A的直线l∥BC,将直线AC绕点D逆时针旋转(旋转角α<∠ACB),分别交直线l于点F与BC的延长线交于点E,连接AE、CF.
如图,在△ABC中∠ACB=90°,D是AC的中点,过点A的直线l∥BC,将直线AC绕点D逆时针旋转(旋转角α<∠ACB),分别交直线l于点F与BC的延长线交于点E,连接AE、CF.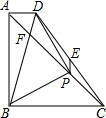 等腰Rt△ABC中,∠ABC=90°,且AB=BC,P为AC上一点,以BP为直角边向上作等腰Rt△BPD,∠BPD=90°.
等腰Rt△ABC中,∠ABC=90°,且AB=BC,P为AC上一点,以BP为直角边向上作等腰Rt△BPD,∠BPD=90°.