题目内容
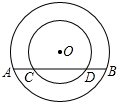 如图,以点O为圆心的两个同心圆,两个圆的半径分别为5cm和9cm,大圆的弦AB交小圆于点C、D且CD=8cm,求AC和BD的长.
如图,以点O为圆心的两个同心圆,两个圆的半径分别为5cm和9cm,大圆的弦AB交小圆于点C、D且CD=8cm,求AC和BD的长.考点:垂径定理,勾股定理
专题:
分析:过O作OE⊥AB于点E,连接OC,OA,根据垂径定理得到AE=BE,CE=DE,从而得到AC=BD,在Rt△OCE中根据勾股定理求出OE的长,同理可得出AE的长,根据AC=AE-CE即可得出结论.
解答: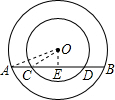 解:作OE⊥AB于点E,连接OC,OA,
解:作OE⊥AB于点E,连接OC,OA,
∵OE⊥AB,CD=8cm,
∴AE=BE,CE=DE=4cm,
∴BE-DE=AE-CE,
∴AC=BD.
在Rt△OCE中,
∵OC=5cm,CE=4cm,
∴OE=
=
=3cm,
在Rt△OAE中,
∵OA=9cm,OE=3cm,
∴AE=
=
=6
cm,
∴AC=BD=(6
-4)cm.
 解:作OE⊥AB于点E,连接OC,OA,
解:作OE⊥AB于点E,连接OC,OA,∵OE⊥AB,CD=8cm,
∴AE=BE,CE=DE=4cm,
∴BE-DE=AE-CE,
∴AC=BD.
在Rt△OCE中,
∵OC=5cm,CE=4cm,
∴OE=
| OC2-CE2 |
| 52-42 |
在Rt△OAE中,
∵OA=9cm,OE=3cm,
∴AE=
| OA2-OE2 |
| 92-32 |
| 2 |
∴AC=BD=(6
| 2 |
点评:本题考查的是垂径定理及勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在△ABC中,∠C=90°,若tanB=
,则sinA=( )
| 5 |
| 12 |
A、
| ||
B、
| ||
C、
| ||
D、
|
 反比例函数y=
反比例函数y=



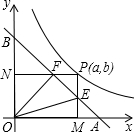 如图,在平面直角坐标系中,直线y=-x+
如图,在平面直角坐标系中,直线y=-x+