题目内容
16.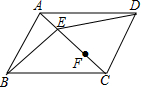 如图,E、F是?ABCD的对角线AC上的两点,且AE=CF,请你以点F为一个端点与图中已标明字母的某一点连成一条线段,猜想并说明它与图中已有的某一条线段相等(只需说明一组线段相等即可).
如图,E、F是?ABCD的对角线AC上的两点,且AE=CF,请你以点F为一个端点与图中已标明字母的某一点连成一条线段,猜想并说明它与图中已有的某一条线段相等(只需说明一组线段相等即可).(1)连结DF;
(2)猜想:BE=DF;
(3)证明:
分析 由平行四边形的性质和已知条件得出OB=OD,OE=OF,证出四边形BEDF是平行四边形,即可得出结论..
解答 (1)解:连接DF;
故答案为:DF;
(2)解:猜想:BE=DF;
故答案为:BE,DF;
(3)证明:连接BF,连接BD,与AC交于点O:
∵四边形ABCD是平行四边形,
∴OB=OD,OA=OC,
∵AE=CF,
∴OA-AE=OC-CF,
∴OE=OF,
∴四边形BEDF是平行四边形,
∴BE=DF.
点评 本题结合平行四边形的性质与判定,证明四边形BEDF是平行四边形是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.学校准备从甲、乙、丙、丁四个小组中选出一组代表学校参加青少年科技创新大赛,各组的平时成绩的平均数(分)及方差如下表所示:
如果要选出一个成绩较好且状态稳定的组去参赛,那么应选的组是( )
| 甲 | 乙 | 丙 | 丁 | |
| $\overline{x}$ | 8 | 9 | 9 | 8 |
| s2 | 1.1 | 1.3 | 1.1 | 1.4 |
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
5.为了了解学生作文考试“书写分”得分情况,李老师随机抽取了10位学生的得分,如图1所示:
(1)利用图1中的信息,补全下表:
(2)李老师把图1转化成图2所示的条形图,请你帮李老师补全条形图;
(3)李老师的学生有60位,请你帮李老师估计得4分以上(含4分)的学生有多少位?
(1)利用图1中的信息,补全下表:
| 平均数(分) | 中位数(分) | 众数(分) |
| 3.4 | 4 | 4 |
(3)李老师的学生有60位,请你帮李老师估计得4分以上(含4分)的学生有多少位?

 △ABC在平面直角坐标系中的位置如图所示,△ABC的顶点均在格点上,其中每个小正方形的边长为1个单位长度,将△ABC绕原点O旋转180°得△A1B1C1.
△ABC在平面直角坐标系中的位置如图所示,△ABC的顶点均在格点上,其中每个小正方形的边长为1个单位长度,将△ABC绕原点O旋转180°得△A1B1C1.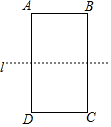 如图,直线l是矩形ABCD的一条对称轴,AD=2AB,点P是直线l上一点,且使得△PAB和△PBC均为等腰三角形,则满足条件的点P共有( )个.
如图,直线l是矩形ABCD的一条对称轴,AD=2AB,点P是直线l上一点,且使得△PAB和△PBC均为等腰三角形,则满足条件的点P共有( )个.