题目内容
11.学校准备从甲、乙、丙、丁四个小组中选出一组代表学校参加青少年科技创新大赛,各组的平时成绩的平均数(分)及方差如下表所示:| 甲 | 乙 | 丙 | 丁 | |
| $\overline{x}$ | 8 | 9 | 9 | 8 |
| s2 | 1.1 | 1.3 | 1.1 | 1.4 |
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
分析 先根据图表找出乙、丙的平均成绩好且相等,再比较它的方差即可得出答案.
解答 解:由图表可知,
乙、丙的平均成绩较好,应从乙、丙中选,
由于S2乙>S2丙,
故乙的方差大,波动大,
则选一个成绩较好且状态稳定的运动员去参赛,应选丙;
故选C.
点评 本题考查了方差,掌握平均数和方差的定义是解题的关键,方差它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.

练习册系列答案
相关题目
1.一个多项式分解因式的结果是x(x-2)2,则该多项式为( )
| A. | x2-2x | B. | x3-2x2 | C. | x2-4x+4 | D. | x3-4x2+4x |
2.一次数学课上,老师让大家在一张长12cm、宽5cm的矩形纸片内,折出一个菱形.甲同学按照取两组对边中点的方法折出菱形EFGH(方案一),乙同学沿矩形的对角线AC折出∠CAE=∠CAD,∠ACF=∠ACB的方法得到菱形AECF(方案二),请你通过计算,比较这两种方案中,折出的菱形面积较大的方案是( )
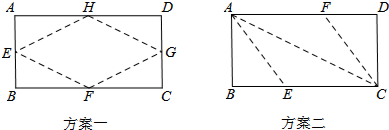

| A. | 方案一 | B. | 方案二 | ||
| C. | 两个方案一样 | D. | 无法通过计算来比较大小 |
1.分式-$\frac{1}{1-x}$可变形为( )
| A. | -$\frac{1}{x-1}$ | B. | -$\frac{1}{1+x}$ | C. | $\frac{1}{1+x}$ | D. | $\frac{1}{x-1}$ |
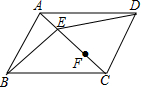 如图,E、F是?ABCD的对角线AC上的两点,且AE=CF,请你以点F为一个端点与图中已标明字母的某一点连成一条线段,猜想并说明它与图中已有的某一条线段相等(只需说明一组线段相等即可).
如图,E、F是?ABCD的对角线AC上的两点,且AE=CF,请你以点F为一个端点与图中已标明字母的某一点连成一条线段,猜想并说明它与图中已有的某一条线段相等(只需说明一组线段相等即可).