题目内容
18.已知两个正数x,y满足x+y=7,则$\sqrt{{x}^{2}+4}+\sqrt{{y}^{2}+9}$的最小值为$\sqrt{74}$.此时x的值为$\frac{14}{5}$.(提示:若借助网格或坐标系,就可以从数形结合的角度来看$\sqrt{{x}^{2}+4}$,例如可以把$\sqrt{{3}^{2}+4}$看做边长为3和4的直角三角形的斜边)分析 先作图构建两个直角三角形:△ACP和△BDP,并作点C关于AB的对称点C′,根据两点之间,线段最短可知$\sqrt{{x}^{2}+4}$+$\sqrt{{y}^{2}+9}$的最小值就是线段C′D的长,并根据平行相似求出x的值.
解答 解::如图所示:AB=7,过A、B两点分别作AB的垂线AC和BD,且AC=2,BD=3.作点C关于AB的对称点C′,连接C′D交AB于P,连接CP,CP=C′P.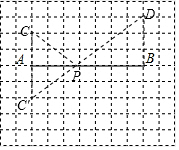
设AP=x,BP=y,则y=7-x,
由勾股定理得:CP=$\sqrt{{x}^{2}+4}$,PD=$\sqrt{{y}^{2}+9}$,
则此时DC′=$\sqrt{{x}^{2}+4}$+$\sqrt{{y}^{2}+9}$的值最小,
∴C′D=C′P+DP=CP+DP=$\sqrt{{7}^{2}+{5}^{2}}$=$\sqrt{74}$.
∵AC′⊥AB,BD⊥AB,
∴AC′∥BD,
∴△APC′∽△BPD,
∴$\frac{AP}{PB}$=$\frac{AC′}{BD′}$,
∴$\frac{x}{7-x}$=$\frac{2}{3}$,
∴x=$\frac{14}{5}$,
故答案为:$\sqrt{74}$;$\frac{14}{5}$.
点评 本题是轴对称的最短路径问题,具体作法是:作某一点的对称点,与另一点相连,所构成的线段长就是最短距离,通常利用勾股定理即可求出.

练习册系列答案
相关题目
9.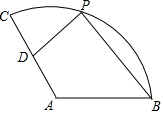 如图,在扇形CAB中,CA=4,∠CAB=120°,D为CA的中点,P为$\widehat{BC}$上一动点(不与C,B重合),则2PD+PB的最小值为( )
如图,在扇形CAB中,CA=4,∠CAB=120°,D为CA的中点,P为$\widehat{BC}$上一动点(不与C,B重合),则2PD+PB的最小值为( )
 如图,在扇形CAB中,CA=4,∠CAB=120°,D为CA的中点,P为$\widehat{BC}$上一动点(不与C,B重合),则2PD+PB的最小值为( )
如图,在扇形CAB中,CA=4,∠CAB=120°,D为CA的中点,P为$\widehat{BC}$上一动点(不与C,B重合),则2PD+PB的最小值为( )| A. | 4+2$\sqrt{3}$ | B. | 4$\sqrt{7}$ | C. | 10 | D. | 4$\sqrt{3}$+4 |
13.估计3+$\sqrt{10}$的运算结果应在( )
| A. | 3到4之间 | B. | 4到5之间 | C. | 5到6之间 | D. | 6到7之间 |
10.下列四个数中,正整数是( )
| A. | -2 | B. | -1 | C. | 0 | D. | 1 |
7. 如图,在平面内直角坐标系中,直线l:y=$\frac{\sqrt{3}}{3}$x+1交x轴于点A,交y轴于点B,点A1,A2,A3,…在x轴上,点B1、B2、B3,…在直线l上.若△OB1A1,△A1B2A2,△A2B3A3,…均为等边三角形,则OAn的长是( )
如图,在平面内直角坐标系中,直线l:y=$\frac{\sqrt{3}}{3}$x+1交x轴于点A,交y轴于点B,点A1,A2,A3,…在x轴上,点B1、B2、B3,…在直线l上.若△OB1A1,△A1B2A2,△A2B3A3,…均为等边三角形,则OAn的长是( )
 如图,在平面内直角坐标系中,直线l:y=$\frac{\sqrt{3}}{3}$x+1交x轴于点A,交y轴于点B,点A1,A2,A3,…在x轴上,点B1、B2、B3,…在直线l上.若△OB1A1,△A1B2A2,△A2B3A3,…均为等边三角形,则OAn的长是( )
如图,在平面内直角坐标系中,直线l:y=$\frac{\sqrt{3}}{3}$x+1交x轴于点A,交y轴于点B,点A1,A2,A3,…在x轴上,点B1、B2、B3,…在直线l上.若△OB1A1,△A1B2A2,△A2B3A3,…均为等边三角形,则OAn的长是( )| A. | 2n$\sqrt{3}$ | B. | (2n+1)$\sqrt{3}$ | C. | (2n-1-1)$\sqrt{3}$ | D. | (2n-1)$\sqrt{3}$ |
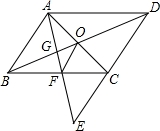 如图,E为?ABCD中DC边的延长线上一点,且CE=DC.判断AB与OF的位置关系和数量关系,并说明理由.
如图,E为?ABCD中DC边的延长线上一点,且CE=DC.判断AB与OF的位置关系和数量关系,并说明理由.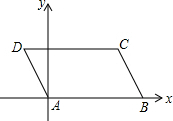 如图,在?ABCD中,AB=5,AD=2,∠DAB=120°,若以点A为原点,直线AB为x轴,建立如图所示的平面直角坐标系,试分别求出B,C,D三点的坐标.
如图,在?ABCD中,AB=5,AD=2,∠DAB=120°,若以点A为原点,直线AB为x轴,建立如图所示的平面直角坐标系,试分别求出B,C,D三点的坐标.


