题目内容
3.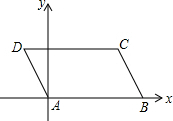 如图,在?ABCD中,AB=5,AD=2,∠DAB=120°,若以点A为原点,直线AB为x轴,建立如图所示的平面直角坐标系,试分别求出B,C,D三点的坐标.
如图,在?ABCD中,AB=5,AD=2,∠DAB=120°,若以点A为原点,直线AB为x轴,建立如图所示的平面直角坐标系,试分别求出B,C,D三点的坐标.
分析 过点D作DE⊥x轴于点E,在Rt△ADE中求出AE、DE,继而可得出点D的坐标,由平行四边形的性质可得点C的坐标.
解答 解:根据题意得:点B的坐标为(5,0),
过点D作DE⊥x轴于点E,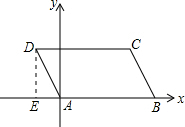 在Rt△ADE中,∠DAE=60°,AD=2,
在Rt△ADE中,∠DAE=60°,AD=2,
∴AE=1,DE=$\sqrt{3}$,
故可得点D的坐标为(-1,$\sqrt{3}$),
又∵四边形ABCD是平行四边形,CD=AB=5,
∴点C的坐标为(4,$\sqrt{3}$);
综上可得:B(5.0)、C(4,$\sqrt{3}$)、D(-1,$\sqrt{3}$).
点评 本题考查了平行四边形的性质及勾股定理的知识,属于基础题,注意掌握平行四边形的对边平行且相等.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
12.在践行社会主义核心价值观活动中,共评选出各级各类“湖北好人”45 000多名.45 000这个数用科学记数法表示为( )
| A. | 4.5×103 | B. | 4.5×104 | C. | 4.5×105 | D. | 0.45×105 |
13.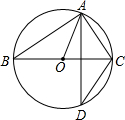 如图,A、D是⊙O上的两个点,BC是直径,若∠D=32°,则∠OAC等于( )
如图,A、D是⊙O上的两个点,BC是直径,若∠D=32°,则∠OAC等于( )
 如图,A、D是⊙O上的两个点,BC是直径,若∠D=32°,则∠OAC等于( )
如图,A、D是⊙O上的两个点,BC是直径,若∠D=32°,则∠OAC等于( )| A. | 64° | B. | 58° | C. | 68° | D. | 55° |
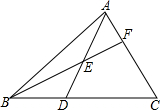 在△ABC中,D在BC上,E在AD上,连结BE,并延长交AC于F,若3BD=2CD,AE=DE,则$\frac{AF}{FC}$=$\frac{2}{5}$.
在△ABC中,D在BC上,E在AD上,连结BE,并延长交AC于F,若3BD=2CD,AE=DE,则$\frac{AF}{FC}$=$\frac{2}{5}$.