题目内容
8.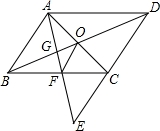 如图,E为?ABCD中DC边的延长线上一点,且CE=DC.判断AB与OF的位置关系和数量关系,并说明理由.
如图,E为?ABCD中DC边的延长线上一点,且CE=DC.判断AB与OF的位置关系和数量关系,并说明理由.
分析 本题可先证明△ABF≌△ECF,从而得出BF=CF,这样就得出了OF是△ABC的中位线,从而利用中位线定理即可得出线段OF与线段AB的关系.
解答 解:AB=2OF.AB∥OF;理由如下:
∵四边形ABCD是平行四边形,
∴AB=CD,OA=OC.
∴∠BAF=∠CEF,∠ABF=∠ECF.
∵CE=DC,
在平行四边形ABCD中,CD=AB,
∴AB=CE.
∴在△ABF和△ECF中,$\left\{\begin{array}{l}{∠BAF=∠CEF}&{\;}\\{AB=CE}&{\;}\\{∠ABF=∠BCF}&{\;}\end{array}\right.$,
∴△ABF≌△ECF(ASA),
∴BF=CF.
∵OA=OC,
∴OF是△ABC的中位线,
∴AB=2OF,AB∥OF.
点评 此题主要考查了平行四边形的性质,全等三角形的性质与判定及三角形的中位线定理,综合的知识点比较多,解答本题的关键是判断出OF是△ABC的中位线.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
18. 两个有理数a,b在数轴上的位置如图所示,则下列关系式成立的是( )
两个有理数a,b在数轴上的位置如图所示,则下列关系式成立的是( )
 两个有理数a,b在数轴上的位置如图所示,则下列关系式成立的是( )
两个有理数a,b在数轴上的位置如图所示,则下列关系式成立的是( )| A. | -a<-b<a<b | B. | a<b<-a<-b | C. | b<-a<a<-b | D. | -b<a<-a<b |
3.在平面直角坐标系中,点A(3,m)在第四象限,若点A关于x轴的对称点B在直线y=-x+4上,则m的值为( )
| A. | 1 | B. | -1 | C. | 2 | D. | -2 |
 如图,已知?ABCD中,AE平分∠BAD交DC于E,DF⊥BC于F,交AE于G,且AD=DF.
如图,已知?ABCD中,AE平分∠BAD交DC于E,DF⊥BC于F,交AE于G,且AD=DF.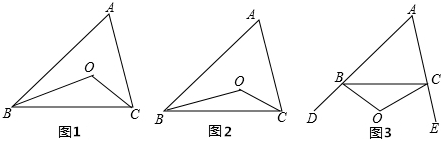
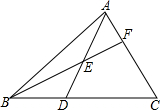 在△ABC中,D在BC上,E在AD上,连结BE,并延长交AC于F,若3BD=2CD,AE=DE,则$\frac{AF}{FC}$=$\frac{2}{5}$.
在△ABC中,D在BC上,E在AD上,连结BE,并延长交AC于F,若3BD=2CD,AE=DE,则$\frac{AF}{FC}$=$\frac{2}{5}$.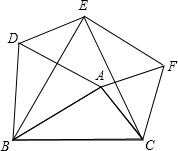 如图,已知△ABD,△BCE,△ACF都是等边三角形,求证:四边形ADEF是平行四边形.
如图,已知△ABD,△BCE,△ACF都是等边三角形,求证:四边形ADEF是平行四边形.