题目内容
7. 如图,在平面内直角坐标系中,直线l:y=$\frac{\sqrt{3}}{3}$x+1交x轴于点A,交y轴于点B,点A1,A2,A3,…在x轴上,点B1、B2、B3,…在直线l上.若△OB1A1,△A1B2A2,△A2B3A3,…均为等边三角形,则OAn的长是( )
如图,在平面内直角坐标系中,直线l:y=$\frac{\sqrt{3}}{3}$x+1交x轴于点A,交y轴于点B,点A1,A2,A3,…在x轴上,点B1、B2、B3,…在直线l上.若△OB1A1,△A1B2A2,△A2B3A3,…均为等边三角形,则OAn的长是( )| A. | 2n$\sqrt{3}$ | B. | (2n+1)$\sqrt{3}$ | C. | (2n-1-1)$\sqrt{3}$ | D. | (2n-1)$\sqrt{3}$ |
分析 根据一次函数图象上点的坐标可得出点A的坐标,由一次函数的解析式可得出∠BOA=30°,结合等边三角形的性质即可得出∠AB1O=∠AB2A1=∠AB3A2=…=30°,进而即可得出OA1、OA2、OA3、OA4的长度,再根据边的变化找出变化规律“OAn=(2n-1)OA=(2n-1)$\sqrt{3}$”,此题得解.
解答 解:∵直线l:y=$\frac{\sqrt{3}}{3}$x+1交x轴于点A,交y轴于点B,
∴∠BOA=30°,点A(-$\sqrt{3}$,0).
∵△OB1A1,△A1B2A2,△A2B3A3,…均为等边三角形,
∴∠AB1O=∠AB2A1=∠AB3A2=…=30°,
∴OA1=OA,OA2=OA1+AA1=3OA,OA3=OA2+AA2=7OA,OA4=OA3+AA3=15OA,…,
∴OAn=(2n-1)OA=(2n-1)$\sqrt{3}$.
故选D.
点评 本题考查了一次函数图象上点的坐标特征、等边三角形的性质以及规律型中数的变化类,根据边的变化找出变化规律“OAn=(2n-1)OA=(2n-1)$\sqrt{3}$”是解题的关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
2.下列各运算中,计算正确的是( )
| A. | (-3ab2)2=9a2b4 | B. | 2a+3b=5ab | C. | $\sqrt{9}$=±3 | D. | (a-b)2=a2-b2 |
12.在践行社会主义核心价值观活动中,共评选出各级各类“湖北好人”45 000多名.45 000这个数用科学记数法表示为( )
| A. | 4.5×103 | B. | 4.5×104 | C. | 4.5×105 | D. | 0.45×105 |
19.下列说法中,正确的是( )
| A. | “打开电视,正在播放新闻联播节目”是必然事件 | |
| B. | 某种彩票中奖概率为10%是指买10张一定有一张中奖 | |
| C. | 了解某种节能灯的使用寿命应采用全面检查 | |
| D. | 一组数据3,5,4,6,7的中位数是5,方差是2 |
16.在平面直角坐标系中,△ABC的三个顶点分别为A(-4,3),B(-6,1),C(-1,1),将△ABC绕着原点O顺时针旋转180°后得到△A1B1C1,则点B的对应点B1的坐标是( )
| A. | (1,-1) | B. | (4,-3) | C. | (-1,-1) | D. | (6,-1) |
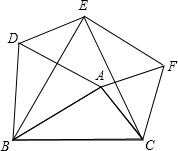 如图,已知△ABD,△BCE,△ACF都是等边三角形,求证:四边形ADEF是平行四边形.
如图,已知△ABD,△BCE,△ACF都是等边三角形,求证:四边形ADEF是平行四边形.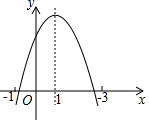 二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法:①b2-4ac=0;②2a+b=0;③若(x1,y1),(x2,y2)在函数图象上,当x1<x2时,y1<y2;④a-b+c<0.其中正确的是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法:①b2-4ac=0;②2a+b=0;③若(x1,y1),(x2,y2)在函数图象上,当x1<x2时,y1<y2;④a-b+c<0.其中正确的是( )