题目内容
2.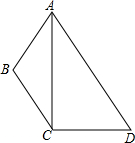 如图,在四边形ABCD中,∠D=60°,∠B是钝角,对角线AC平分∠BAD.
如图,在四边形ABCD中,∠D=60°,∠B是钝角,对角线AC平分∠BAD.(1)若BC∥AD,∠ACD=85°,求∠B;
(2)若BC=CD,求∠B.
分析 (1)由BC∥AD,得到∠ACB=∠DAC,由于对角线AC平分∠BAD,得到∠BAC=∠CAD,等量代换得到∠BAC=∠ACB,根据三角形的内角和得到∠DAC=35°,即可得到结论;
(2)过C作CE⊥AB交AB的延长线于E,CF⊥AD于F,根据角平分线的性质得到CE=CF,推出Rt△CBE≌Rt△CDF,根据全等三角形的性质得到∠CBE=∠D=60°,即可得到结论.
解答 解:(1)∵BC∥AD,
∴∠ACB=∠DAC,
∵对角线AC平分∠BAD,
∴∠BAC=∠CAD,
∴∠BAC=∠ACB,
∵∠ACD=85°,∠D=60°,
∴∠DAC=35°,
∴∠BAC=∠ACB=35°,
∴∠B=180°-35°-35°=110°;
(2)过C作CE⊥AB交AB的延长线于E,CF⊥AD于F,
∵对角线AC平分∠BAD,
∴CE=CF,
在Rt△CBE与Rt△CDF中,$\left\{\begin{array}{l}{CE=CF}\\{CB=CD}\end{array}\right.$,
∴Rt△CBE≌Rt△CDF,
∴∠CBE=∠D=60°,
∴∠ABC=180°-60°=120°.
点评 本题考查了全等三角形的判定和性质,角平分线的性质,等腰三角形的判定和性质,正确的作出辅助线是解题的关键.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
 如图,如果把△ABC的顶点A先向下平移3格,再向左平移1格到达A′点,连接A′B,则线段A′B与线段AC的位置关系是互相垂直平分.
如图,如果把△ABC的顶点A先向下平移3格,再向左平移1格到达A′点,连接A′B,则线段A′B与线段AC的位置关系是互相垂直平分.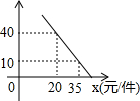 学生小李在暑假进行社会实践活动,准备采购一批学习用品进行销售,进货时老板告诉小李,每件商品可以优惠2元,这样原价330元的商品现在可以多买1件还余10元.
学生小李在暑假进行社会实践活动,准备采购一批学习用品进行销售,进货时老板告诉小李,每件商品可以优惠2元,这样原价330元的商品现在可以多买1件还余10元.