题目内容
9．
如图，△ABC中，∠B=90°，BC=2AB，则cosA=$\frac{\sqrt{5}}{5}$．
分析 根据勾股定理，可得AC的长，根据余弦等于邻边比斜边，可得答案．
解答 解：由勾股定理，得
AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{5}$AB，
cosA=$\frac{AB}{AC}$=$\frac{AB}{\sqrt{5}AB}$=$\frac{\sqrt{5}}{5}$，
故答案为：$\frac{\sqrt{5}}{5}$．
点评 本题考查锐角三角函数的定义及运用：在直角三角形中，锐角的正弦为对边比斜边，余弦为邻边比斜边，正切为对边比邻边．
练习册系列答案
相关题目
我市某风景区门票价格如图所示，百姓旅行社有甲、乙两个旅行团队，计划在“五一”小黄金周期间到该景点游玩，两团队游客人数之和为120人，乙团队人数不超过50人．设甲团队人数为x人，如果甲、乙两团队分别购买门票，两团队门票款之和为W元．
4．下列四个命题：
①垂直于弦的直径平分弦所对的两条弧；
②在同圆或等圆中，相等的弦所对的圆 周角相等；
③三角形有且只有一个外接圆；
④任意三角形是内心总是在三角形的内部；
⑤三角形的外心到三角形三边的距离相等．
其中真命题的个数有（ ）
①垂直于弦的直径平分弦所对的两条弧；
②在同圆或等圆中，相等的弦所对的圆 周角相等；
③三角形有且只有一个外接圆；
④任意三角形是内心总是在三角形的内部；
⑤三角形的外心到三角形三边的距离相等．
其中真命题的个数有（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
1．
一次函数y=kx+b的图象如图，则当0＜x≤1时，y的范围是（ ）
一次函数y=kx+b的图象如图，则当0＜x≤1时，y的范围是（ ）| A． | y＞0 | B． | -2＜y≤0 | C． | -2＜y≤1 | D． | 无法判断 |
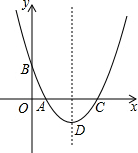如图，已知二次函数y=x2+bx+c的图象关于直线x=2对称，且与x轴交于A、C两点，与y轴交于点B，点C与坐标原点不重合，其坐标为（c，0）．
19．下列运动属于数学上的旋转的有（ ）
| A． | 钟表上的时针运动 | B． | 城市环路公共汽车 | ||
| C． | 地球绕太阳转动 | D． | 将等腰三角形沿着底边上的高对折 |