题目内容
已知抛物线的顶点(-1,-2)且图象经过(1,6),
(1)求该二次函数的解析式;
(2)当y>0时,x的取值范围.
(1)求该二次函数的解析式;
(2)当y>0时,x的取值范围.
考点:待定系数法求二次函数解析式
专题:
分析:(1)根据抛物线的顶点坐标(-1,-2),所以设此二次函数的解析式为y=a(x+1)2-2,把点(1,6)代入解析式即可解答.
(2)先求得抛物线与x轴的交点,即可求得自变量x的取值范围.
(2)先求得抛物线与x轴的交点,即可求得自变量x的取值范围.
解答:解:(1)已知抛物线的顶点坐标为M(1,-2),
设此二次函数的解析式为y=a(x+1)2-2,
把点(1,6)代入解析式,得:
4a-2=6,即a=2,
∴此函数的解析式为y=2(x+1)2-2.
(2)当y=0时,2(x+1)2-2=0,
解得x=0或x=-2,
∴抛物线与x轴的交点为(-2,0),(0,0),
∵y>0时,函数的图象位于x轴的上方,
∴图象位于x轴的上方的自变量x的取值范围为x<-2,或x>0.
设此二次函数的解析式为y=a(x+1)2-2,
把点(1,6)代入解析式,得:
4a-2=6,即a=2,
∴此函数的解析式为y=2(x+1)2-2.
(2)当y=0时,2(x+1)2-2=0,
解得x=0或x=-2,
∴抛物线与x轴的交点为(-2,0),(0,0),
∵y>0时,函数的图象位于x轴的上方,
∴图象位于x轴的上方的自变量x的取值范围为x<-2,或x>0.
点评:本题考查了用待定系数法求函数解析式的方法.若题目给出了二次函数的顶点坐标,则采用顶点式求解简单.

练习册系列答案
相关题目
 如图,AB是半圆的直径,P是半圆上的一点,PD⊥AB于点D,若AD=8,DB=2,则PD=( )
如图,AB是半圆的直径,P是半圆上的一点,PD⊥AB于点D,若AD=8,DB=2,则PD=( )| A、2 | ||
| B、4 | ||
C、2
| ||
D、4
|
某机械厂一月份生产零件50万个,计划通过改革技术,使今后两月的产量都比前一月增长一个相同的百分数,使得三月份生产零件72万个.若设这个百分数为x,则可列方程为( )
| A、50(1+x)2=72 |
| B、50+50(1+x)2=72 |
| C、50(1+x)+50(1+x)2=72 |
| D、50+50(1+x)+50(1+x)2=72 |
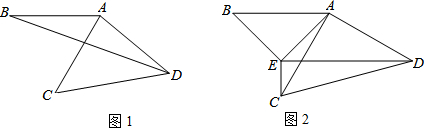
 如图是一块菜地,已知CD=6m,AD=8m,∠ADC=90°,CB=24m,AB=26m,你能求出这块菜地的面积吗?
如图是一块菜地,已知CD=6m,AD=8m,∠ADC=90°,CB=24m,AB=26m,你能求出这块菜地的面积吗?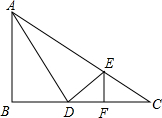 如图,在△ABC中,∠B=90°,AB=8,BC=16,D在边BC上,BD=6,AD⊥DE交AC于点E,EF⊥BC于点F.
如图,在△ABC中,∠B=90°,AB=8,BC=16,D在边BC上,BD=6,AD⊥DE交AC于点E,EF⊥BC于点F.