题目内容
计算:
(1)1
×(2
-
)-
×
+
;
(2)24×(
+
+…+
)-(
+
+
+…+
).
(1)1
| 4 |
| 17 |
| 2 |
| 3 |
| 3 |
| 4 |
6
| ||||
3
|
| 13 |
| 33 |
17+
| ||
1-
|
(2)24×(
| 1 |
| 2×3 |
| 1 |
| 4×5 |
| 1 |
| 24×25 |
| 1 |
| 12 |
| 1 |
| 12+22 |
| 1 |
| 12+22+32 |
| 1 |
| 12+22+…+122 |
考点:有理数无理数的概念与运算
专题:计算题
分析:(1)只需将带分数化成假分数后,运用有理数的运算法则就可解决问题.
(2))由12+22+32+…+n2=
n(n+1)(2n+1)可得
=
=
=12[
-
],然后运用裂项相消法就可解决问题.
(2))由12+22+32+…+n2=
| 1 |
| 6 |
| 1 |
| 12+22+…+n2 |
| 6 |
| n(n+1)(2n+1) |
| 24 |
| 2n(2n+1)(2n+2) |
| 1 |
| 2n(2n+1) |
| 1 |
| (2n+1)(2n+2) |
解答:解:(1)原式=
×
-
×
+
=
-2×
×
+(17+
)×
=
-2×
×
+21+
=
-2×
×
+21
=3.5-1+21
=23.5.
(2)∵12+22+32+…+n2=
n(n+1)(2n+1),
∴
=
=
=12[
-
]
∴原式=24×(
+
+…+
)-12×(
-
+
-
+…+
-
)
=24×(
+
+…+
)-12×(
+
+…+
)+12×(
+
+…+
)
=12×(
+
+…+
)+12×(
+
+…+
)
=12×(
+
+
+
+…+
+
)
=12×(
-
+
-
+
-
+
-
+…+
-
+
-
)
=12×(
-
)
=12×
=
.
| 21 |
| 17 |
| 23 |
| 12 |
| ||||
|
| 13 |
| 33 |
17+
| ||
|
=
| 7×23 |
| 17×4 |
| ||||
|
| 13 |
| 33 |
| 11 |
| 12 |
| 21 |
| 17 |
=
| 7×23 |
| 17×4 |
| ||
|
| 13 |
| 33 |
| 11×7 |
| 17×4 |
=
| 34×7 |
| 17×4 |
| 33 |
| 26 |
| 13 |
| 33 |
=3.5-1+21
=23.5.
(2)∵12+22+32+…+n2=
| 1 |
| 6 |
∴
| 1 |
| 12+22+…+n2 |
| 6 |
| n(n+1)(2n+1) |
| 24 |
| 2n(2n+1)(2n+2) |
=12[
| 1 |
| 2n(2n+1) |
| 1 |
| (2n+1)(2n+2) |
∴原式=24×(
| 1 |
| 2×3 |
| 1 |
| 4×5 |
| 1 |
| 24×25 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 4×5 |
| 1 |
| 5×6 |
| 1 |
| 24×25 |
| 1 |
| 25×26 |
=24×(
| 1 |
| 2×3 |
| 1 |
| 4×5 |
| 1 |
| 24×25 |
| 1 |
| 2×3 |
| 1 |
| 4×5 |
| 1 |
| 24×25 |
| 1 |
| 3×4 |
| 1 |
| 5×6 |
| 1 |
| 25×26 |
=12×(
| 1 |
| 2×3 |
| 1 |
| 4×5 |
| 1 |
| 24×25 |
| 1 |
| 3×4 |
| 1 |
| 5×6 |
| 1 |
| 25×26 |
=12×(
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 4×5 |
| 1 |
| 5×6 |
| 1 |
| 24×25 |
| 1 |
| 25×26 |
=12×(
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 5 |
| 1 |
| 6 |
| 1 |
| 24 |
| 1 |
| 25 |
| 1 |
| 25 |
| 1 |
| 26 |
=12×(
| 1 |
| 2 |
| 1 |
| 26 |
=12×
| 6 |
| 13 |
=
| 72 |
| 13 |
点评:本题主要考查了有理数的运算,运用公式12+22+32+…+n2=
n(n+1)(2n+1),并采用裂项相消法是解决第(2)小题的关键.
| 1 |
| 6 |

练习册系列答案
相关题目
 如图,AB是⊙O的直径,DC是弦,若∠BDC=31°,则∠COB的度数等于( )
如图,AB是⊙O的直径,DC是弦,若∠BDC=31°,则∠COB的度数等于( )| A、64° | B、60° |
| C、62° | D、65° |
与3a2b是同类项的是( )
| A、a2 |
| B、2ab |
| C、3ab2 |
| D、4ba2 |
已知x=2是方程(3x-m)(x+3)=0的一个根,则m的值为( )
| A、6 | B、-6 | C、2 | D、-2 |
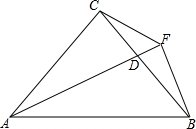 在Rt△ABC中,∠ACB=90°,AC=BC.
在Rt△ABC中,∠ACB=90°,AC=BC.