题目内容
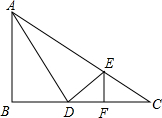 如图,在△ABC中,∠B=90°,AB=8,BC=16,D在边BC上,BD=6,AD⊥DE交AC于点E,EF⊥BC于点F.
如图,在△ABC中,∠B=90°,AB=8,BC=16,D在边BC上,BD=6,AD⊥DE交AC于点E,EF⊥BC于点F.(1)填空:图中相似三角形有
(2)求线段FC的长;
(3)过点D的直线分别交直线AB、线段AE于G、H,是否存在这样的直线,使△AGH与△CDH相似?若存在,求AG的长;若不存在,请说明理由.
考点:相似三角形的判定与性质
专题:
分析:(1)根据题意结合图形即可判断出有两对相似三角形.
(2)设出线段FC、EF的长度,运用相似三角形的性质列出两对比例式,进而构造出了两个方程,解方程组即可解决问题.
(3)经比较、分析,若△AGH与△CDH相似,只有△AGH∽△DCH;利用相似三角形的性质列出比例式求出BG的长,进而求出AB的长.
(2)设出线段FC、EF的长度,运用相似三角形的性质列出两对比例式,进而构造出了两个方程,解方程组即可解决问题.
(3)经比较、分析,若△AGH与△CDH相似,只有△AGH∽△DCH;利用相似三角形的性质列出比例式求出BG的长,进而求出AB的长.
解答:解:(1)如图,
∵∠B=90°,AD⊥DE,EF⊥BC,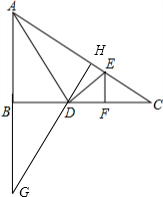
∴∠BAD+∠ADB=∠ADB+∠EDF,
∴∠BAD=∠EDF,而∠B=∠EFD,
∴△ABD∽△DFE;
又∵∠B=∠EFD,∠C=∠C,
∴△ABC∽△EFC;
故答案为:△ABD∽△DFE,△ABC∽△EFC.
(2)∵BC=16,BD=6,
∴DC=16-6=10;
设FC=x,EF=y,则DF=10-x;
∵由(1)知△ABD∽△DFE,
∴
=
,即
=
,
∴4y=30-3x①;
又∵由(1)知△ABC∽△EFC,
∴
=
,即
=
,
∴2y=x②;
联立①、②并解得x=6,y=3,
故线段FC的长为6.
(3)存在这样的直线GH,使△AGH与△CDH相似;
∵∠DHC>∠GAH,
∴若△AGH与△CDH相似,必有∠EDH=∠BAH,
此时,A、B、D、H四点公圆;
∴∠AHD=180°-∠ABD=90°,
即GH⊥AC;
∴当GH⊥AC时,△AGH∽△DCH;
∵GH⊥AC,∠B=90°,
∴∠G+∠BAH=∠C+∠BAH,
∴∠G=∠C;
又∵∠GBD=∠CBA,
∴△BGD∽△CBA,
∴
=
,即
=
,
∴BG=12,AG=8+12=20,
即AG的长为20.
∵∠B=90°,AD⊥DE,EF⊥BC,

∴∠BAD+∠ADB=∠ADB+∠EDF,
∴∠BAD=∠EDF,而∠B=∠EFD,
∴△ABD∽△DFE;
又∵∠B=∠EFD,∠C=∠C,
∴△ABC∽△EFC;
故答案为:△ABD∽△DFE,△ABC∽△EFC.
(2)∵BC=16,BD=6,
∴DC=16-6=10;
设FC=x,EF=y,则DF=10-x;
∵由(1)知△ABD∽△DFE,
∴
| AB |
| DF |
| BD |
| EF |
| 8 |
| 10-x |
| 6 |
| y |
∴4y=30-3x①;
又∵由(1)知△ABC∽△EFC,
∴
| AB |
| EF |
| BC |
| CF |
| 8 |
| y |
| 16 |
| x |
∴2y=x②;
联立①、②并解得x=6,y=3,
故线段FC的长为6.
(3)存在这样的直线GH,使△AGH与△CDH相似;
∵∠DHC>∠GAH,
∴若△AGH与△CDH相似,必有∠EDH=∠BAH,
此时,A、B、D、H四点公圆;
∴∠AHD=180°-∠ABD=90°,
即GH⊥AC;
∴当GH⊥AC时,△AGH∽△DCH;
∵GH⊥AC,∠B=90°,
∴∠G+∠BAH=∠C+∠BAH,
∴∠G=∠C;
又∵∠GBD=∠CBA,
∴△BGD∽△CBA,
∴
| BG |
| BC |
| BD |
| AB |
| BG |
| 16 |
| 6 |
| 8 |
∴BG=12,AG=8+12=20,
即AG的长为20.
点评:该题考查了相似三角形的判定及其性质的应用问题;解题的关键是准确找出相似三角形,灵活运用性质解题.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
 在Rt△ABC中,∠ACB=90°,AC=BC.
在Rt△ABC中,∠ACB=90°,AC=BC.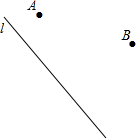 如图,直线l表示一条公路,点A、B表示两个村庄,现要在公路l上建一个加油站.并使加油站到两村庄A、B的距离相等.加油站应建在何处?在图中标出加油站位置,并说明理由.
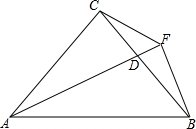
如图,直线l表示一条公路,点A、B表示两个村庄,现要在公路l上建一个加油站.并使加油站到两村庄A、B的距离相等.加油站应建在何处?在图中标出加油站位置,并说明理由. 如图,已知AB=DE,BC=EF,AF=DC,则∠B=∠E,请说明理由(填空)
如图,已知AB=DE,BC=EF,AF=DC,则∠B=∠E,请说明理由(填空) 如图所示,a,b为有理数,则a+b
如图所示,a,b为有理数,则a+b