题目内容
10. 如图,正方形ANCD和正方形EFGH的边长都为1,E是正方ABCD的中心,两正方形重合部分的面积是$\frac{1}{4}$.
如图,正方形ANCD和正方形EFGH的边长都为1,E是正方ABCD的中心,两正方形重合部分的面积是$\frac{1}{4}$.
分析 连接DE,CE,根据正方形的性质得出ED=EC,∠EDM=∠ECN=45°,∠DEC=∠NEM=90°,推出∠DEM=∠CEN,从而证出△EDM≌△ECN,则两正方形重合部分的面积是正方形ABCD面积的$\frac{1}{4}$,问题得解.
解答 解:连接DE,CE,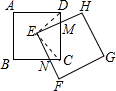
∵四边形ABCD和四边形EFGH都是正方形,
∴ED=EC,∠EDM=∠ECN=45°,∠DEC=∠NEM=90°,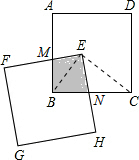
∴∠DEM=∠CEN.
在△EDM与△ECN中,
$\left\{\begin{array}{l}{∠EDM=∠ECN}\\{DE=CE}\\{∠DEM=∠CEN}\end{array}\right.$,
∴△EDM≌△ECN(ASA),
∴四边形EMCN的面积等于三角形DEC的面积,
∴重叠部分面积不变,总是等于正方形面积的$\frac{1}{4}$,
即$\frac{1}{4}$×1×1=$\frac{1}{4}$.
故答案为$\frac{1}{4}$.
点评 本题主要考查对正方形的性质,全等三角形的性质和判定等知识点的理解和掌握,能推出四边形EMCN的面积等于三角形DEC的面积是解此题的关键.

练习册系列答案
相关题目
20.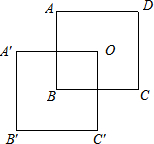 将大小相同的两个正方形纸片按如图所示方式叠放在一起,已知正方形的边长为2,点O为正方形的中心,至少平移几个单位长度才能使两个正方形完全重合?( )
将大小相同的两个正方形纸片按如图所示方式叠放在一起,已知正方形的边长为2,点O为正方形的中心,至少平移几个单位长度才能使两个正方形完全重合?( )
 将大小相同的两个正方形纸片按如图所示方式叠放在一起,已知正方形的边长为2,点O为正方形的中心,至少平移几个单位长度才能使两个正方形完全重合?( )
将大小相同的两个正方形纸片按如图所示方式叠放在一起,已知正方形的边长为2,点O为正方形的中心,至少平移几个单位长度才能使两个正方形完全重合?( )| A. | $\sqrt{2}$ | B. | 2 | C. | 2$\sqrt{2}$ | D. | 4 |
1.南浔红蜻蜓鞋店销售不同尺寸的鞋子,现对鞋子销售情况如下作调查,下面的调查数据中,店主最值得关注的是( )
| A. | 平均数 | B. | 方差 | C. | 中位数 | D. | 众数 |
 如图,平行四边形ABCD中,AB=3,BC=8,延长BA到E,使得AE=1,连接EC交AD于点F,则DF=6.
如图,平行四边形ABCD中,AB=3,BC=8,延长BA到E,使得AE=1,连接EC交AD于点F,则DF=6.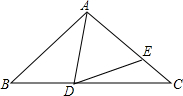 如图,在等腰三角形ABC中,AB=AC,等边三角形ADE的顶点D,E分别落在AC,AC上,若AD=BD,求∠EDC的度数.
如图,在等腰三角形ABC中,AB=AC,等边三角形ADE的顶点D,E分别落在AC,AC上,若AD=BD,求∠EDC的度数.