题目内容
5. 如图,平行四边形ABCD中,AB=3,BC=8,延长BA到E,使得AE=1,连接EC交AD于点F,则DF=6.
如图,平行四边形ABCD中,AB=3,BC=8,延长BA到E,使得AE=1,连接EC交AD于点F,则DF=6.
分析 在平行四边形ABCD中,由AB∥CD,CD=AB=3,AD=BC=8,于是得到△AEF∽△CDF,求得$\frac{AE}{CD}=\frac{AE}{DF}$,代入数值即可得到结论.
解答 解:∵在平行四边形ABCD中,
∴AB∥CD,CD=AB=3,AD=BC=8,
∴△AEF∽△CDF,
∴$\frac{AE}{CD}=\frac{AE}{DF}$,
∴$\frac{1}{3}=\frac{8-DF}{DF}$,
解得:DF=6,
故答案为:6.
点评 此题考查了相似三角形的判定与性质以及平行四边形的性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
 如图,梯形ABCD是拦水坝的横断面图(图中i=$1:\sqrt{3}$是指坡面的垂直高度DE与水平宽度CE的比)∠B=60°,AB=6cm,AD=5cm,求拦水坝的横断面ABCD的面积(结果保留三位有效数字,参考数据:$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414)
如图,梯形ABCD是拦水坝的横断面图(图中i=$1:\sqrt{3}$是指坡面的垂直高度DE与水平宽度CE的比)∠B=60°,AB=6cm,AD=5cm,求拦水坝的横断面ABCD的面积(结果保留三位有效数字,参考数据:$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414) 如图,正方形ANCD和正方形EFGH的边长都为1,E是正方ABCD的中心,两正方形重合部分的面积是$\frac{1}{4}$.
如图,正方形ANCD和正方形EFGH的边长都为1,E是正方ABCD的中心,两正方形重合部分的面积是$\frac{1}{4}$.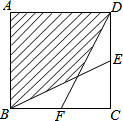 如图,正方形ABCD的边长为1cm,E、F分别是BC、CD的中点,连接BF、DE,则图中阴影部分的面积是$\frac{2}{3}$ cm2.
如图,正方形ABCD的边长为1cm,E、F分别是BC、CD的中点,连接BF、DE,则图中阴影部分的面积是$\frac{2}{3}$ cm2.