题目内容
18.解方程:$\frac{x}{x+3}$-1=$\frac{2}{x-3}$.分析 分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:去分母得:x2-3x-x2+9=2x+6,
解得:x=$\frac{3}{5}$,
经检验x=$\frac{3}{5}$是分式方程的解.
点评 此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.

练习册系列答案
相关题目
3.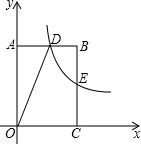 如图,双曲线y=$\frac{k}{x}$(k>0)经过矩形OABC的边BC的中点E,交AB于点D.若矩形OABC的面积为6,则双曲线的解析式为( )
如图,双曲线y=$\frac{k}{x}$(k>0)经过矩形OABC的边BC的中点E,交AB于点D.若矩形OABC的面积为6,则双曲线的解析式为( )
 如图,双曲线y=$\frac{k}{x}$(k>0)经过矩形OABC的边BC的中点E,交AB于点D.若矩形OABC的面积为6,则双曲线的解析式为( )
如图,双曲线y=$\frac{k}{x}$(k>0)经过矩形OABC的边BC的中点E,交AB于点D.若矩形OABC的面积为6,则双曲线的解析式为( )| A. | y=$\frac{1}{x}$ | B. | y=$\frac{2}{x}$ | C. | y=$\frac{3}{x}$ | D. | y=$\frac{6}{x}$ |
7.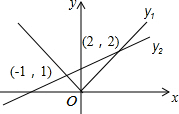 函数y1=|x|,y2=$\frac{1}{3}$x+$\frac{4}{3}$.当y1<y2时,x的范围是( )
函数y1=|x|,y2=$\frac{1}{3}$x+$\frac{4}{3}$.当y1<y2时,x的范围是( )
 函数y1=|x|,y2=$\frac{1}{3}$x+$\frac{4}{3}$.当y1<y2时,x的范围是( )
函数y1=|x|,y2=$\frac{1}{3}$x+$\frac{4}{3}$.当y1<y2时,x的范围是( )| A. | x<-1 | B. | -1<x<2 | C. | x<-1或x>2 | D. | x>2 |
8.下列计算正确的是( )
| A. | 2x+3y=5xy | B. | y3÷y3=1 | C. | $\sqrt{2}+\sqrt{3}=\sqrt{5}$ | D. | -$\sqrt{(-4)^{2}}$=-4 |
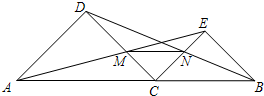 如图,已知C是线段AB上的任意一点(除端点外),分别以AC、BC为斜边并且在AB的同一侧作等腰直角△ACD和△BCE,连接AE交CD于点M,连接BD交CE于点N.
如图,已知C是线段AB上的任意一点(除端点外),分别以AC、BC为斜边并且在AB的同一侧作等腰直角△ACD和△BCE,连接AE交CD于点M,连接BD交CE于点N. 如图,正方形ANCD和正方形EFGH的边长都为1,E是正方ABCD的中心,两正方形重合部分的面积是$\frac{1}{4}$.
如图,正方形ANCD和正方形EFGH的边长都为1,E是正方ABCD的中心,两正方形重合部分的面积是$\frac{1}{4}$.