题目内容
20.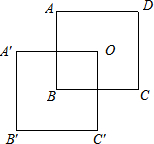 将大小相同的两个正方形纸片按如图所示方式叠放在一起,已知正方形的边长为2,点O为正方形的中心,至少平移几个单位长度才能使两个正方形完全重合?( )
将大小相同的两个正方形纸片按如图所示方式叠放在一起,已知正方形的边长为2,点O为正方形的中心,至少平移几个单位长度才能使两个正方形完全重合?( )| A. | $\sqrt{2}$ | B. | 2 | C. | 2$\sqrt{2}$ | D. | 4 |
分析 连接BD,则点O在BD上,由四边形ABCD 是正方形,于是得到∠A=90°,AB=AD=2,BO=OD,由勾股定理得到BD=2$\sqrt{2}$,求得OD=$\sqrt{2}$,于是得到结论.
解答 解:连接BD,则点O在BD上,
四边形ABCD 是正方形,
∴∠A=90°,AB=AD=2,BO=OD,
∴BD=2$\sqrt{2}$,
∴OD=$\sqrt{2}$,
∴至少平移$\sqrt{2}$个单位长度才能使两个正方形完全重合.
故选:A.
点评 本题考查了平移的性质,正方形的性质,熟记平移的性质是解题的关键.

练习册系列答案
相关题目
5. 如图,笑脸盖住的点的坐标可能为( )
如图,笑脸盖住的点的坐标可能为( )
 如图,笑脸盖住的点的坐标可能为( )
如图,笑脸盖住的点的坐标可能为( )| A. | (5,2) | B. | (-2,3) | C. | (-4,-2) | D. | (3,-4) |
 如图,抛物线y=-x2+bx+c经过点A(1,0),C(4,0),与y轴交于点B.
如图,抛物线y=-x2+bx+c经过点A(1,0),C(4,0),与y轴交于点B.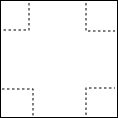 小明用边长为16厘米的正方形纸片制作一个无盖的长方体形纸盒,他在正方形纸片的四个角上剪去边长为4厘米的小正方形(如图),这样折成的无盖长方体纸盒的容积是多少?
小明用边长为16厘米的正方形纸片制作一个无盖的长方体形纸盒,他在正方形纸片的四个角上剪去边长为4厘米的小正方形(如图),这样折成的无盖长方体纸盒的容积是多少?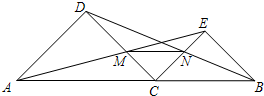 如图,已知C是线段AB上的任意一点(除端点外),分别以AC、BC为斜边并且在AB的同一侧作等腰直角△ACD和△BCE,连接AE交CD于点M,连接BD交CE于点N.
如图,已知C是线段AB上的任意一点(除端点外),分别以AC、BC为斜边并且在AB的同一侧作等腰直角△ACD和△BCE,连接AE交CD于点M,连接BD交CE于点N. 如图,正方形ANCD和正方形EFGH的边长都为1,E是正方ABCD的中心,两正方形重合部分的面积是$\frac{1}{4}$.
如图,正方形ANCD和正方形EFGH的边长都为1,E是正方ABCD的中心,两正方形重合部分的面积是$\frac{1}{4}$.