题目内容
(1)比较下列两个算式的结果的大小(在横线上选填“>”“=”或“<”)
①32+42 2×3×4;
②(
)2+(
)2 2×
×
;
③(-2)2+(-3)2 2×(-2)×(-3);
④(-
)2+(-
)2 2×(-
)×(-
);
⑤(-4)2+(-4)2 2×(-4)×(-4).
(2)观察并归纳(1)中的规律,用含a,b的一个关系式把你的发现表示出来.
(3)若已知ab=8,且a,b都是正数,试求
a2+
b2的最小值.
①32+42
②(
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 4 |
③(-2)2+(-3)2
④(-
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 3 |
| 1 |
| 5 |
⑤(-4)2+(-4)2
(2)观察并归纳(1)中的规律,用含a,b的一个关系式把你的发现表示出来.
(3)若已知ab=8,且a,b都是正数,试求
| 1 |
| 2 |
| 1 |
| 2 |
考点:完全平方公式
专题:规律型
分析:(1)两式计算得到结果,即可做出判断;
(2)归纳总结得到一般性规律,写出即可;
(3)利用得出的规律求出原式的最小值即可.
(2)归纳总结得到一般性规律,写出即可;
(3)利用得出的规律求出原式的最小值即可.
解答:解:(1)①32+42>2×3×4;
②(
)2+(
)2>2×
×
;
③(-2)2+(-3)2>2×(-2)×(-3);
④(-
)2+(-
)2>2×(-
)×(-
);
⑤(-4)2+(-4)2=2×(-4)×(-4).
故答案为:①>;②>;③>;④>;⑤=;
(2)a2+b2≥2ab;
(3)∵ab=8,且a,b都是正数,
∴
a2+
b2=
(a2+b2)≥
×2ab=ab=8,
则当a=b=2
时,
a2+
b2的最小值为8.
②(
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 4 |
③(-2)2+(-3)2>2×(-2)×(-3);
④(-
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 3 |
| 1 |
| 5 |
⑤(-4)2+(-4)2=2×(-4)×(-4).
故答案为:①>;②>;③>;④>;⑤=;
(2)a2+b2≥2ab;
(3)∵ab=8,且a,b都是正数,
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
则当a=b=2
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:此题考查了完全平方公式,熟练掌握公式是解本题的关键.

练习册系列答案
相关题目
 a、b、c在数轴上的位置如图所示,且|a|=|b|,试求|a-c|-|c-b|+|a+b+c|的值.
a、b、c在数轴上的位置如图所示,且|a|=|b|,试求|a-c|-|c-b|+|a+b+c|的值.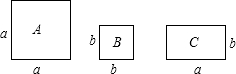 如图,正方形卡片A类、B类和长方形卡片C类各若干张(a≠b),如果要选用上述3类卡片共12张拼成一个大长方形(拼接时不可重叠,不可有缝隙)、且卡片全部用上,则不同的选取方案有
如图,正方形卡片A类、B类和长方形卡片C类各若干张(a≠b),如果要选用上述3类卡片共12张拼成一个大长方形(拼接时不可重叠,不可有缝隙)、且卡片全部用上,则不同的选取方案有 如图,在边长为6cm正方形ABCD中,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC和CD边向D点以2cm/s的速度移动,如果点P、Q分别从A、B同时出发,其中一点到终点,另一点也随之停止.过了
如图,在边长为6cm正方形ABCD中,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC和CD边向D点以2cm/s的速度移动,如果点P、Q分别从A、B同时出发,其中一点到终点,另一点也随之停止.过了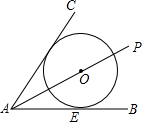 如图所示,已知PA是∠BAC的平分线,AB是⊙O的切线,切点为E,求证:AC是⊙O的切线.
如图所示,已知PA是∠BAC的平分线,AB是⊙O的切线,切点为E,求证:AC是⊙O的切线. 如图,AB=7,C是线段AB上一点,D是线段BC的中点,图中所有线段的和是23,求线段AC的长?
如图,AB=7,C是线段AB上一点,D是线段BC的中点,图中所有线段的和是23,求线段AC的长?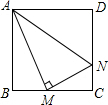 如图,正方形ABCD的边长为6,M、N分别是BC、CD上的两个动点,当点M在BC边上运动时,始终保持AM⊥MN.
如图,正方形ABCD的边长为6,M、N分别是BC、CD上的两个动点,当点M在BC边上运动时,始终保持AM⊥MN.