题目内容
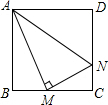 如图,正方形ABCD的边长为6,M、N分别是BC、CD上的两个动点,当点M在BC边上运动时,始终保持AM⊥MN.
如图,正方形ABCD的边长为6,M、N分别是BC、CD上的两个动点,当点M在BC边上运动时,始终保持AM⊥MN.(1)请你找出图中一对相似三角形,并加以证明;
(2)当点M运动到什么位置时,线段CN的长度最大?求出此时BM和CN的值.
考点:正方形的性质,相似三角形的判定与性质
专题:
分析:(1)利用正方形的性质进而得出得出对应角之间关系进而求出即可;
(2)利用相似三角形的性质进而结合二次函数最值求法得出即可.
(2)利用相似三角形的性质进而结合二次函数最值求法得出即可.
解答:(1)答:△ABM∽△MCN,
证明:∵AM⊥MN,
∴∠AMN=90°,
∴∠AMB+∠CMN=90°,
∵∠B+∠C=90°,
∴∠AMB+∠BAM=90°,
∴∠BAM=∠CMN,
∴△ABM∽△MCN;
(2)解:设BM=x,由(1)知,△ABM∽△MCN,
∴
=
,即
=
,
则CN=
x(6-x)=-
(x-3)2+
,
故当x=3时,即点M在BC的中点时,线段CN的长度最大,
此时,BM=3,CN=
.
证明:∵AM⊥MN,
∴∠AMN=90°,
∴∠AMB+∠CMN=90°,
∵∠B+∠C=90°,
∴∠AMB+∠BAM=90°,
∴∠BAM=∠CMN,
∴△ABM∽△MCN;
(2)解:设BM=x,由(1)知,△ABM∽△MCN,
∴
| AB |
| MC |
| BM |
| CN |
| 6 |
| 6-x |
| x |
| CN |
则CN=
| 1 |
| 6 |
| 1 |
| 6 |
| 3 |
| 2 |
故当x=3时,即点M在BC的中点时,线段CN的长度最大,
此时,BM=3,CN=
| 3 |
| 2 |
点评:此题主要考查了相似三角形的判定与性质以及正方形的性质,熟练应用相似三角形的性质是解题关键.

练习册系列答案
相关题目
下面图形中是轴对称图形的是( )
A、 |
B、 |
C、 |
D、 |
将点P(m+2,2m+4)向下平移3个单位长度,向右平移1个单位长度,得到点P′,且点P′在y轴上,那么点P′的坐标为( )
| A、(0,-3) |
| B、(0,-5) |
| C、(0,-2) |
| D、(-5,0) |
下列说法正确的是( )
| A、33ab2的次数是6次 | ||
B、
| ||
C、-
| ||
| D、x2+x-1的常数项是1 |
下列计算正确的是( )
| A、-2x2-3x2=-5x2 |
| B、2x2-3x2=-x |
| C、a2+a3=a5 |
| D、3a2b-3ab2=0 |
 如图,已知∠BOF=130°,则∠A+∠B+∠C+∠D+∠E+∠F=
如图,已知∠BOF=130°,则∠A+∠B+∠C+∠D+∠E+∠F=