题目内容
20．
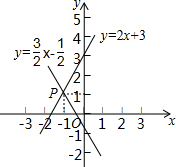如图，函数y=-$\frac{3}{2}$x-$\frac{1}{2}$和y=2x+3的图象交于点P，则根据图象可得，二元一次方程组$\left\{\begin{array}{l}{y=2x+3}\\{y=-\frac{3}{2}x-\frac{1}{2}}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=-1}\\{y=1}\end{array}\right.$．
分析 观察函数图象找出两函数图象交点坐标，由此即可得出方程组的解．
解答 解：观察函数图象可知：交点P的坐标为（-1，1），
∴二元一次方程组$\left\{\begin{array}{l}{y=2x+3}\\{y=-\frac{3}{2}x-\frac{1}{2}}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=-1}\\{y=1}\end{array}\right.$．
故答案为：$\left\{\begin{array}{l}{x=-1}\\{y=1}\end{array}\right.$．
点评 本题考查了一次函数与二元一次方程组，熟练掌握联立两函数解析式所成的方程组的解即是两函数图象的交点坐标是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
如图，在长30m，宽20m的矩形地面上修建两条同样宽的道路，余下部分作为绿化带，已知绿化带的面积为551m2，求所修建道路的宽度．
10．
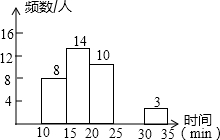某校中午学生用餐比较拥挤，为建议学校分年级错时用餐，李老师带领数学学习小组在某天随机调查了部分学生，统计了他们从下课到就餐结束所用的时间，并绘制成统计表和如图所示的不完整统计图．
根据以上提供的信息，解答下列问题：
（1）表中a=35%，b=5，c=40，补全频数分布直方图；
（2）此次调查中，中位数所在的时间段是15≤x＜20min．
（3）这所学校共有1200人，试估算从下课到就餐结束所用时间不少于20min的共有多少人？
某校中午学生用餐比较拥挤，为建议学校分年级错时用餐，李老师带领数学学习小组在某天随机调查了部分学生，统计了他们从下课到就餐结束所用的时间，并绘制成统计表和如图所示的不完整统计图．根据以上提供的信息，解答下列问题：
（1）表中a=35%，b=5，c=40，补全频数分布直方图；
（2）此次调查中，中位数所在的时间段是15≤x＜20min．
| 时间分段/min | 频（人）数 | 百分比 |
| 10≤x＜15 | 8 | 20% |
| 15≤x＜20 | 14 | a |
| 20≤x＜25 | 10 | 25% |
| 25≤x＜30 | b | 12.50% |
| 30≤x＜35 | 3 | 7.50% |
| 合计 | c | 100% |