题目内容
3.在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,设BC=a,AC=b,若AB=16,CD=6,则a-b=±8.分析 由勾股定理和三角形面积关系得出a2+b2=c2=256,ab=96,得出(a-b)2=a2+b2-2ab=64,由平方根定义即可得出结果.
解答 解:∵∠ACB=90°,
∴a2+b2=c2=256,
∵CD⊥AB,
∴△ABC的面积=$\frac{1}{2}$ab=$\frac{1}{2}$×16×6,
∴ab=96,
∴(a-b)2=a2+b2-2ab=256-2×96=64,
∴a-b=±8;
故答案为:±8.
点评 本题考查了勾股定理、三角形的面积关系、完全平方公式以及平方根定义;熟练掌握勾股定理是解决问题的关键.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
15.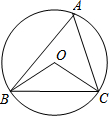 如图,⊙O的半径为2,△ABC是⊙O的内接三角形,连结OB,OC,若∠BAC与∠BOC互补,则弦BC的长为( )
如图,⊙O的半径为2,△ABC是⊙O的内接三角形,连结OB,OC,若∠BAC与∠BOC互补,则弦BC的长为( )
 如图,⊙O的半径为2,△ABC是⊙O的内接三角形,连结OB,OC,若∠BAC与∠BOC互补,则弦BC的长为( )
如图,⊙O的半径为2,△ABC是⊙O的内接三角形,连结OB,OC,若∠BAC与∠BOC互补,则弦BC的长为( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 2$\sqrt{2}$ | D. | 4 |
 如图,在平行四边形ABCD中,EF∥AB交AD于E交BD于F,DE:EA=3:4,EF=6,则CD的长为14.
如图,在平行四边形ABCD中,EF∥AB交AD于E交BD于F,DE:EA=3:4,EF=6,则CD的长为14. 如图放置的△OAB1,△B1A1B2,△B2A2B3,…都是边长为1的等边三角形,点A在x轴上,点O,B1,B2,B3,…都在直线l上,则点A2的坐标是(2,$\sqrt{3}$),点A2017的坐标是($\frac{2019}{2}$,$\frac{2017\sqrt{3}}{2}$).
如图放置的△OAB1,△B1A1B2,△B2A2B3,…都是边长为1的等边三角形,点A在x轴上,点O,B1,B2,B3,…都在直线l上,则点A2的坐标是(2,$\sqrt{3}$),点A2017的坐标是($\frac{2019}{2}$,$\frac{2017\sqrt{3}}{2}$).