题目内容
13.通分:(1)$\frac{x}{6a{b}^{2}}$,$\frac{y}{9{a}^{2}bc}$;
(2)$\frac{1}{{x}^{2}-16}$,$\frac{1}{2x-8}$.
分析 (1)找出两分母的最简公分母即可
(2)先将分母进行因式分解,然后再找出最简公分母.
解答 解:(1)最简公分母为:18a2b2c,
∴$\frac{x}{6a{b}^{2}}$×$\frac{3ac}{3ac}$=$\frac{3acx}{18{a}^{2}{b}^{2}c}$
$\frac{y}{{9a}^{2}bc}×\frac{2b}{2b}$=$\frac{2by}{18{{a}^{2}b}^{2}c}$
(2)两分式的分母为:(x+4)(x-4)、2(x-4)
∴最简公分母为:2(x+4)(x-4)
∴$\frac{1}{(x-4)(x+4)}$×$\frac{2}{2}$=$\frac{2}{2(x+4)(x-4)}$,
$\frac{1}{2(x-4)}$×$\frac{x+4}{x+4}$=$\frac{x+4}{2(x+4)(x-4)}$
点评 本题考查通分,解题的关键是找出各分母的最简公分母,本题属于基础题型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.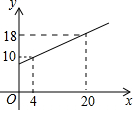 若弹簧的总长度y(cm)是所挂重物x(千克)的一次函数图象如图,则不挂重物时,弹簧的长度是( )
若弹簧的总长度y(cm)是所挂重物x(千克)的一次函数图象如图,则不挂重物时,弹簧的长度是( )
 若弹簧的总长度y(cm)是所挂重物x(千克)的一次函数图象如图,则不挂重物时,弹簧的长度是( )
若弹簧的总长度y(cm)是所挂重物x(千克)的一次函数图象如图,则不挂重物时,弹簧的长度是( )| A. | 5cm | B. | 8cm | C. | 9cm | D. | 10cm |
5.独山县各学校开展了第二课堂的活动,在某校国学诗词组、篮球足球组、陶艺茶艺组三个活动组织中,若小斌和小宇两名同学每人随机选择其中一个活动参加,则小斌和小宇选到同一活动的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{9}$ |
 如图,给正五边形的顶点依次编号为1,2,3,4,5.若从某一顶点开始,沿正五边形的边顺时针方向行走,顶点编号的数字是几,就走几个边长,则称这种走法为一次“移位”.如:小宇在编号为3的顶点上时,那么他应走3个边长,即从3→4→5→1为第一次“移位”,这时他到达编号为1的顶点;然后从1→2为第二次“移位”.若小宇从编号为2的顶点开始,第20次“移位”后,则他所处顶点的编号为1.
如图,给正五边形的顶点依次编号为1,2,3,4,5.若从某一顶点开始,沿正五边形的边顺时针方向行走,顶点编号的数字是几,就走几个边长,则称这种走法为一次“移位”.如:小宇在编号为3的顶点上时,那么他应走3个边长,即从3→4→5→1为第一次“移位”,这时他到达编号为1的顶点;然后从1→2为第二次“移位”.若小宇从编号为2的顶点开始,第20次“移位”后,则他所处顶点的编号为1.
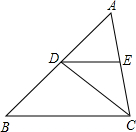 如图,CD平分∠ACB,∠AED=80°,∠DCB=40°,DE与BC平行吗?试说明理由.
如图,CD平分∠ACB,∠AED=80°,∠DCB=40°,DE与BC平行吗?试说明理由.