题目内容
2.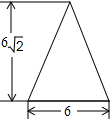 如图,是一圆锥的左视图,根据图中所标数据,圆锥侧面展开图的扇形圆心角的大小为( )
如图,是一圆锥的左视图,根据图中所标数据,圆锥侧面展开图的扇形圆心角的大小为( )| A. | 90° | B. | 120° | C. | 135° | D. | 150° |
分析 根据圆锥的底面半径得到圆锥的底面周长,也就是圆锥的侧面展开图的弧长,根据勾股定理得到圆锥的母线长,利用弧长公式可求得圆锥的侧面展开图中扇形的圆心角.
解答 解:∵圆锥的底面半径为3,
∴圆锥的底面周长为6π,
∵圆锥的高是6$\sqrt{2}$,
∴圆锥的母线长为$\sqrt{{3}^{2}+(6\sqrt{2})^{2}}$=9,
设扇形的圆心角为n°,
∴$\frac{nπ×9}{180}$=6π,
解得n=120.
答:圆锥的侧面展开图中扇形的圆心角为120°.
故选B.
点评 本题考查了圆锥的计算,圆锥的侧面展开图是一个扇形,此扇形的弧长等于圆锥底面周长,扇形的半径等于圆锥的母线长.本题就是把的扇形的弧长等于圆锥底面周长作为相等关系,列方程求解.

练习册系列答案
相关题目
13.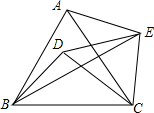 如图,点D在等边△ABC内,将△ABC绕点C顺时针旋转60°,得到△ACE,连接BE、DE,若∠AEB=45°,则∠DBE的度数为( )
如图,点D在等边△ABC内,将△ABC绕点C顺时针旋转60°,得到△ACE,连接BE、DE,若∠AEB=45°,则∠DBE的度数为( )
 如图,点D在等边△ABC内,将△ABC绕点C顺时针旋转60°,得到△ACE,连接BE、DE,若∠AEB=45°,则∠DBE的度数为( )
如图,点D在等边△ABC内,将△ABC绕点C顺时针旋转60°,得到△ACE,连接BE、DE,若∠AEB=45°,则∠DBE的度数为( )| A. | 15° | B. | 20° | C. | 25° | D. | 30° |
11.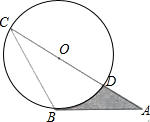 如图,AB是⊙O的切线,B为切点,AC经过点O,与⊙O分别相交于点D,C.若∠ACB=30°,AB=$\sqrt{3}$,则阴影部分的面积是( )
如图,AB是⊙O的切线,B为切点,AC经过点O,与⊙O分别相交于点D,C.若∠ACB=30°,AB=$\sqrt{3}$,则阴影部分的面积是( )
 如图,AB是⊙O的切线,B为切点,AC经过点O,与⊙O分别相交于点D,C.若∠ACB=30°,AB=$\sqrt{3}$,则阴影部分的面积是( )
如图,AB是⊙O的切线,B为切点,AC经过点O,与⊙O分别相交于点D,C.若∠ACB=30°,AB=$\sqrt{3}$,则阴影部分的面积是( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{π}{6}$ | C. | $\frac{\sqrt{3}}{2}$-$\frac{π}{6}$ | D. | $\frac{\sqrt{3}}{3}$-$\frac{π}{6}$ |
12.已知x1、x2是一元二次方程3x2=6-2x的两根,则x1-x1x2+x2的值是( )
| A. | $-\frac{4}{3}$ | B. | $\frac{8}{3}$ | C. | $-\frac{8}{3}$ | D. | $\frac{4}{3}$ |
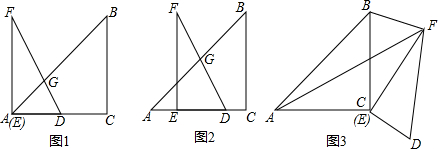
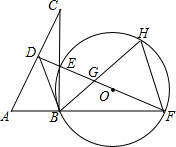 如图,在Rt△ABC中,∠ABC=90°,AC的垂直平分线分别与AC,BC及AB的延长线相交于点D,E,F,⊙O是△BEF的外接圆,∠EBF的平分线交EF于点G,交⊙O于点H,连接BD、FH.
如图,在Rt△ABC中,∠ABC=90°,AC的垂直平分线分别与AC,BC及AB的延长线相交于点D,E,F,⊙O是△BEF的外接圆,∠EBF的平分线交EF于点G,交⊙O于点H,连接BD、FH.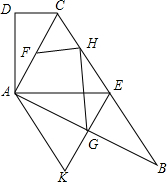 如图,在四边形ABCD中,AC平分∠BCD,AC⊥AB,E是BC的中点,AD⊥AE.
如图,在四边形ABCD中,AC平分∠BCD,AC⊥AB,E是BC的中点,AD⊥AE.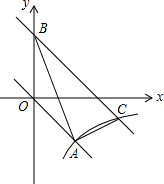 如图,在平面直角坐标xOy中,正比例函数y=kx的图象与反比例函数y=$\frac{m}{x}$的图象都经过点A(2,-2).
如图,在平面直角坐标xOy中,正比例函数y=kx的图象与反比例函数y=$\frac{m}{x}$的图象都经过点A(2,-2).