题目内容
17.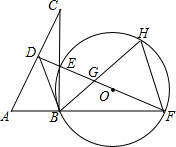 如图,在Rt△ABC中,∠ABC=90°,AC的垂直平分线分别与AC,BC及AB的延长线相交于点D,E,F,⊙O是△BEF的外接圆,∠EBF的平分线交EF于点G,交⊙O于点H,连接BD、FH.
如图,在Rt△ABC中,∠ABC=90°,AC的垂直平分线分别与AC,BC及AB的延长线相交于点D,E,F,⊙O是△BEF的外接圆,∠EBF的平分线交EF于点G,交⊙O于点H,连接BD、FH.(1)试判断BD与⊙O的位置关系,并说明理由;
(2)当AB=BE=1时,求⊙O的面积;
(3)在(2)的条件下,求HG•HB的值.
分析 (1)连接OB,证得∠DBO=90°,即可得到BD与⊙O相切;
(2)由等腰直角三角形的性质得到CF=$\sqrt{2}$BF,由于DF垂直平分AC,得到AF=CF=AB+BF=1+BF=$\sqrt{2}$BF,根据勾股定理得到EF的长,根据圆的面积公式即可得到结论;
(3)推出△EHF是等腰直角三角形,求得HF=$\frac{\sqrt{2}}{2}$EF,通过△BHF∽△FHG,列比例式即可得到结论.
解答  解:(1)BD与⊙O相切,
解:(1)BD与⊙O相切,
理由:如图1,连接OB,
∵OB=OF,
∴∠OBF=∠OFB,
∵∠ABC=90°,AD=CD,
∴BD=CD,
∴∠C=∠DBC,
∵∠C=∠BFE,
∴∠DBC=∠OBF,
∵∠CBO+∠OBF=90°,
∴∠DBC+∠CBO=90°,
∴∠DBO=90°,
∴BD与⊙O相切;
(2)如图2,连接CF,HE,
∵∠CDE=90°,∠ABC=90°,
∴∠DEC=∠A,
∵∠CED=∠FEB,
∴∠FEB=∠A.
∵AB=BE,∠ABC=∠CBF=90°,
∴△ABC≌△EBF, ∵BC=BF,
∵BC=BF,
∴CF=$\sqrt{2}$BF,
∵DF垂直平分AC,
∴AF=CF=AB+BF=1+BF=$\sqrt{2}$BF,
∴BF=$\sqrt{2}$+1,
∴EF=$\sqrt{B{F}^{2}+B{E}^{2}}$=$\sqrt{4+2\sqrt{2}}$,
∵∠CBF=90°,
∴EF是⊙O的直径,
∴⊙O的面积=($\frac{1}{2}$EF)2•π=$\frac{4+2\sqrt{2}}{4}$π=$\frac{2+\sqrt{2}}{2}$π;
(3)∵BH平分∠CBF,
∴$\widehat{EH}$=$\widehat{HF}$,
∴EH=FH,
∴△EHF是等腰直角三角形,
∴HF=$\frac{\sqrt{2}}{2}$EF=$\sqrt{2+\sqrt{2}}$,
∵∠EFH=∠HBF=45°,∠BHF=∠BHF,
∴△BHF∽△FHG,
∴$\frac{HF}{HG}=\frac{BH}{HF}$,
∴HG•HB=HF2=2+$\sqrt{2}$.
点评 本题考查了全等三角形的判定和性质,相似三角形的判定和性质,圆周角定理,勾股定理,线段的垂直平分线的性质,直角三角形的性质,等腰直角三角形的判定和性质,熟练掌握这些定理是解题的关键.

| A. | 3.6 元 | B. | 5 元 | C. | 10 元 | D. | 12 元 |
| A. | k≥1 | B. | k>1 | C. | k≥-1 | D. | k>-1 |
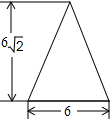 如图,是一圆锥的左视图,根据图中所标数据,圆锥侧面展开图的扇形圆心角的大小为( )
如图,是一圆锥的左视图,根据图中所标数据,圆锥侧面展开图的扇形圆心角的大小为( )| A. | 90° | B. | 120° | C. | 135° | D. | 150° |
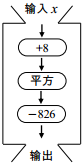 输入一组数据,按下列程序进行计算,输出结果如表:
输入一组数据,按下列程序进行计算,输出结果如表:| x | 20.5 | 20.6 | 20.7 | 20.8 | 20.9 |
| 输出 | -13.75 | -8.04 | -2.31 | 3.44 | 9.21 |
| A. | 20.5<x<20.6 | B. | 20.6<x<20.7 | C. | 20.7<x<20.8 | D. | 20.8<x<20.9 |
| A. | -2016 | B. | $\frac{1}{2016}$ | C. | 2016 | D. | $-\frac{1}{2016}$ |
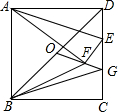 如图,在正方形ABCD中,AB=6,点E在边CD上,DE=$\frac{1}{3}$DC,连接AE,将△ADE沿AE翻折,点D落在点F处,点O是对角线BD的中点,连接OF并延长OF交CD于点G,连接BF,BG,则△BFG的周长是$\frac{12}{5}$($\sqrt{5}$+$\sqrt{10}$).
如图,在正方形ABCD中,AB=6,点E在边CD上,DE=$\frac{1}{3}$DC,连接AE,将△ADE沿AE翻折,点D落在点F处,点O是对角线BD的中点,连接OF并延长OF交CD于点G,连接BF,BG,则△BFG的周长是$\frac{12}{5}$($\sqrt{5}$+$\sqrt{10}$). 已知△ABN和△ACM位置如图所示,AB=AC,AD=AE,∠1=∠2.
已知△ABN和△ACM位置如图所示,AB=AC,AD=AE,∠1=∠2.