题目内容
18．
在?ABCD中，DE⊥AC、BF⊥AC，连接BE、DF．求证：四边形DEBF是平行四边形．
分析 欲证明四边形DEBF是平行四边形，只要证明DE=BF，DE∥BF即可．
解答 证明∵四边形ABCD为平行四边形，
∴AD=CB，AD∥BC，∠DAC=∠BCA，
又∵DE⊥AC BF⊥AC
∴∠DEA=∠BFC=90°，DE∥BF，
在△ADE和△CBF中，
$\left\{\begin{array}{l}{∠DAE=∠BCF}\\{∠DEA=∠BFC}\\{AD=BC}\end{array}\right.$，
∴△ADE≌△CBF，
∴DE=BF，
∴四边形DEBF是平行四边形．
点评 本题考查平行四边形的判定和性质、全等三角形的判定和性质等知识，解题的关键是记住平行四边形的判定方法，证明方法比较多，属于中考常考题型．
练习册系列答案
相关题目
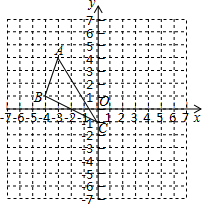如图，在平面直角坐标系中，△ABC三个顶点的坐标分别为A（-3，4），B（-4，1），C（0，-1）．将△ABC向右平移4个单位长度，再向下平移3个单位长度，得到△A′B′C′，其中点A′，B′，C′分别为点A，B，C的对应点．
如图，已知△ABC≌△DEB，点E在AB上，DE与AC相交于点F，