题目内容
7.已知:四边形ABCD是菱形,两条对角线的长分别为AC=10,BD=24,则边长AB的长为13.分析 由平行四边形的性质,可得OA=$\frac{1}{2}$AC=12,OB=$\frac{1}{2}$BD=5,AC⊥BD,继而利用勾股定理,求得这个菱形的边长.
解答 解:
∵四边形ABCD是菱形,
∴OA=$\frac{1}{2}$AC=12,OB=$\frac{1}{2}$BD=12,AC⊥BD,
∴AB=$\sqrt{A{O}^{2}+B{O}^{2}}$=13,
故答案为:13.
点评 本题考查了菱形对角线互相垂直平分的性质,考查了菱形各边长相等的性质,考查了勾股定理在直角三角形中的运用,根据勾股定理求AB的值是解题的关键.

练习册系列答案
相关题目
2.为了了解某市4万多名初中毕业生的中考数学成绩,任意抽取1000名学生的中考数学成绩进行统计分析,这个问题中,1000是( )
| A. | 总体 | B. | 样本 | C. | 个体 | D. | 样本容量 |
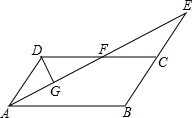 如图,在平行四边形ABCD中,∠BAD的平分线与BC的延长线交于点E,与DC交于点F.
如图,在平行四边形ABCD中,∠BAD的平分线与BC的延长线交于点E,与DC交于点F. 在?ABCD中,DE⊥AC、BF⊥AC,连接BE、DF.求证:四边形DEBF是平行四边形.
在?ABCD中,DE⊥AC、BF⊥AC,连接BE、DF.求证:四边形DEBF是平行四边形.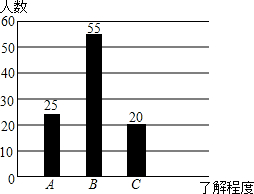 某中学组织学生开展社会实践活动,调查某社区居民对消防知识的了解程度(A:特别熟悉,B:有所了解,C:不知道),在该社区随机抽取了100名居民进行问卷调查,将调查结果制成如图所示的统计图,根据统计图解答下列问题:
某中学组织学生开展社会实践活动,调查某社区居民对消防知识的了解程度(A:特别熟悉,B:有所了解,C:不知道),在该社区随机抽取了100名居民进行问卷调查,将调查结果制成如图所示的统计图,根据统计图解答下列问题: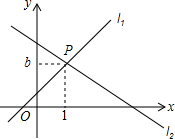 如图,直线l1:y=x+1与直线l2:y=mx+n相交于点P(1,b).
如图,直线l1:y=x+1与直线l2:y=mx+n相交于点P(1,b). 如图,直线a∥b,射线DF与直线a相交于点C,过点D作DE⊥b于点E,已知∠1=25°,求∠2的度数.
如图,直线a∥b,射线DF与直线a相交于点C,过点D作DE⊥b于点E,已知∠1=25°,求∠2的度数.