题目内容
6.为绿化校园,某校计划购进A、B两种树苗,共21课.已知A种树苗每棵90元,B种树苗每棵70元.设购买B种树苗x棵,购买两种树苗所需费用为y元.(1)求y与x的函数表达式;
(2)若购买B种树苗的数量少于A种树苗的数量,请给出一种费用最省的方案,并求出该方案所需费用.
分析 (1)设购买B种树苗x棵,则购买A种树苗(21-x)棵,根据“总费用=A种树苗的单价×购买A种树苗棵树+B种树苗的单价×购买B种树苗棵树”即可得出y关于x的函数关系式;
(2)根据购买B种树苗的数量少于A种树苗的数量可得出关于x的一元一次不等式,解不等式即可求出x的取值范围,再结合一次函数的性质即可得出结论.
解答 解:(1)设购买B种树苗x棵,则购买A种树苗(21-x)棵,
由已知得:y=70x+90(21-x)=-20x+1890(x为整数且0≤x≤21).
(2)由已知得:x<21-x,
解得:x<$\frac{21}{2}$.
∵y=-20x+1890中-20<0,
∴当x=10时,y取最小值,最小值为1690.
答:费用最省的方案为购买A种树苗11棵,B种树苗10棵,此时所需费用为1690元.
点评 本题考查了一次函数的应用、解一元一次不等式以及一次函数的性质,解题的关键是:(1)根据数量关系列出y关于x的函数关系式;(2)根据数量关系列出关于x的一元一次不等式.本题属于基础题,难度不大,解决该题型题目时,根据数量关系列出方程(不等式或函数关系式)是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.下列各组线段中,能组成三角形的是( )
| A. | 2,2,4 | B. | 5,6,12 | C. | 6,9,12 | D. | 5,15,8 |
1.一次函数y=3x-6的图象与x轴的交点坐标是( )
| A. | (0,-6) | B. | (0,6) | C. | (2,0) | D. | (-2,0) |
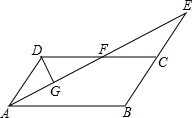 如图,在平行四边形ABCD中,∠BAD的平分线与BC的延长线交于点E,与DC交于点F.
如图,在平行四边形ABCD中,∠BAD的平分线与BC的延长线交于点E,与DC交于点F. 如图,点D,E分别是△ABC的BC,AC边的中点,若AB=2,则DE的长1.
如图,点D,E分别是△ABC的BC,AC边的中点,若AB=2,则DE的长1. 在?ABCD中,DE⊥AC、BF⊥AC,连接BE、DF.求证:四边形DEBF是平行四边形.
在?ABCD中,DE⊥AC、BF⊥AC,连接BE、DF.求证:四边形DEBF是平行四边形.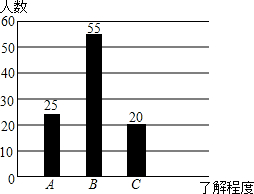 某中学组织学生开展社会实践活动,调查某社区居民对消防知识的了解程度(A:特别熟悉,B:有所了解,C:不知道),在该社区随机抽取了100名居民进行问卷调查,将调查结果制成如图所示的统计图,根据统计图解答下列问题:
某中学组织学生开展社会实践活动,调查某社区居民对消防知识的了解程度(A:特别熟悉,B:有所了解,C:不知道),在该社区随机抽取了100名居民进行问卷调查,将调查结果制成如图所示的统计图,根据统计图解答下列问题: