题目内容
2. 如图,在△ABC中,∠ACB=90°,∠ABC=60°,BD平分∠ABC,P点是BD的中点.若AD=7,则CP的长为( )
如图,在△ABC中,∠ACB=90°,∠ABC=60°,BD平分∠ABC,P点是BD的中点.若AD=7,则CP的长为( )| A. | 3 | B. | 3.5 | C. | 4 | D. | 4.5 |
分析 由题意推出BD=AD,然后在Rt△BCD中,CP=$\frac{1}{2}$BD,即可推出CP的长度.
解答 解:∵∠ACB=90°,∠ABC=60°,
∴∠A=30°,
∵BD平分∠ABC,
∴∠CBD=∠DBA=30°,
∴BD=AD,
∵AD=7,
∴BD=7,
∵P点是BD的中点,
∴CP=$\frac{1}{2}$BD=3.5.
故选B.
点评 本题主要考查角平分线的性质、等腰三角形的判定和性质、折角三角形斜边上的中线的性质,关键在于根据已知推出BD=AD,求出BD的长度.

练习册系列答案
相关题目
12. 如图,已知∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上;△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形.若OA1=1,则△A2015B2015A2016的边长为( )
如图,已知∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上;△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形.若OA1=1,则△A2015B2015A2016的边长为( )
 如图,已知∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上;△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形.若OA1=1,则△A2015B2015A2016的边长为( )
如图,已知∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上;△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形.若OA1=1,则△A2015B2015A2016的边长为( )| A. | 4028 | B. | 4030 | C. | 22014 | D. | 22015 |
13.某商场实行8折优惠销售,现售价为x元的商品的原价是( )
| A. | 0.2x | B. | 0.8x | C. | 1.25x | D. | 5x |
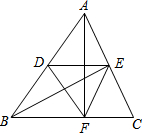 如图,已知在△ABC中,AB=BC=8,AC=6,AF⊥BC于点F,BE⊥AC于点E,取AB的中点D,则△DEF的周长为11.
如图,已知在△ABC中,AB=BC=8,AC=6,AF⊥BC于点F,BE⊥AC于点E,取AB的中点D,则△DEF的周长为11.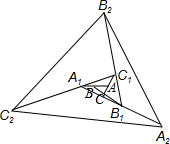 如图,△ABC面积为1,第一次操作:分别延长AB,BC,CA至点A1,B1,C1,使A1B=AB、B1C=2BC,C1A=2CA,顺次连接A1,B1,C1,得到△A1B1C1.第二次操作:分别延长A1B1,B1C1、C1A1至点A2,B2,C2,使A2B1=A1B1,B2C1=2B1C1,C2A1=2C1A1,顺次连接A2,B2,C2,得到△A2B2C2,…按此规律,经过2015次操作后△A2015B2015C2015的面积为142015.
如图,△ABC面积为1,第一次操作:分别延长AB,BC,CA至点A1,B1,C1,使A1B=AB、B1C=2BC,C1A=2CA,顺次连接A1,B1,C1,得到△A1B1C1.第二次操作:分别延长A1B1,B1C1、C1A1至点A2,B2,C2,使A2B1=A1B1,B2C1=2B1C1,C2A1=2C1A1,顺次连接A2,B2,C2,得到△A2B2C2,…按此规律,经过2015次操作后△A2015B2015C2015的面积为142015.