题目内容

11．若矩形ABCD的两邻边长分别为一元二次方程x2-6x+4=0的两个实数根，则矩形ABCD的周长为12．

分析 利用根与系数的关系得出两根和为6，即是矩形ABCD的两邻边长，然后利用周长计算公式求得答案即可．

解答 解：∵设矩形ABCD的两邻边长分别为α、β是一元二次方程x2-6x+4=0的两个实数根，
∴α+β=6，
∴矩形ABCD的周长为6×2=12．
故答案为：12．

点评 本题考查了一元二次方程ax2+bx+c=0（a≠0）的根与系数的关系：若方程两个为x1，x2，则x1+x2=-$\frac{b}{a}$，x1•x2=$\frac{c}{a}$．

练习册系列答案
相关题目
1．把方程3x（x-2）=4（x+1）化为一元二次方程的一般形式是3x2-10x-4=0，它的一次项系数是-10．
2．如图，在△ABC中，∠ACB=90°，∠ABC=60°，BD平分∠ABC，P点是BD的中点．若AD=7，则CP的长为（　　）
A．3B．3.5C．4D．4.5
19．根据所给条件求锐角∠α．（精确到1″）
（1）已知sinα=0.4771，求∠α；
（2）已知cosα=0.8451，求∠α；
（3）已知tanα=1.4106，求∠α．
6．计算：
（1）$\sqrt{196}+\root{3}{8}-\sqrt{25}$
（2）$-\sqrt{36}+\sqrt{2\frac{1}{4}}+\root{3}{27}$．
16．一个长方形的周长为6a+8b，若一边长为2a+b，则它的另一边长为（　　）
A．4a+5bB．a+bC．a+3bD．a+7b
3．阅读下列材料并解决有关问题：
我们知道|x|=$\left\{\begin{array}{l}{x（x＞0）}\\{0（x=0）}\\{-x（x＜0）}\end{array}\right.$现在我们可以用这一结论来化简含有绝对值的代数式，如化简代数式|x+1|+|x-2|时，可令x+1=0和x-2=0，分别求得x=-1和x=2（称-1，2分别为|x+1|与|x-2|的零点值）．在有理数范围内，零点值x=-1和x=2可将全体有理数分成不重复且不遗漏的如下3种情况：（1）x＜-1；（2）-1≤x＜2；（3）x≥2．从而化简代数式|x+1|+|x-2|可分以下3种情况：
（1）当x＜-1时，原式=-（x+1）-（x-2）=-2x+1；
（2）当-1≤x＜2时，原式=x+1-（x-2）=3；
（3）当x≥2时，原式=x+1+x-2=2x-1．
综上讨论，原式=$\left\{\begin{array}{l}{-2x+1（x＜-1）}\\{2（-1≤x＜2）}\\{2x-1（x≥2）}\end{array}\right.$
通过以上阅读，请你解决以下问题：
（1）分别求出|x+2|和|x-4|的零点值；
（2）化简代数式|x+2|+|x-4|；
（3）解方程|x+2|+|x-4|=8．
20．小李上星期五买进某公司股票1000股，每股26元，本表为本周内该股票的涨跌情况（单位：元）
星期一二三四五
每日跌涨+4+4.5-1-2.5-6
（1）周三收盘时，李先生所持股票每股多少元？
（2）本周内，股票最高价出现在星期几？是多少元？
（3）已知小李买进股票是付了0.15%的手续费，卖出时需付成交额的0.15%的手续费，若小李在本周五收盘时卖出全部股票，他的收益如何？
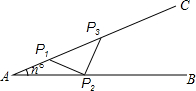1．如图钢架中，∠A=n°，依次焊上等长的钢条P1P2，P2P3，…，来加固钢架，若P1A=P1P2，要使得这样的钢条只能焊上4根，则n的取值范围是18≤n＜22.5．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网