题目内容
7.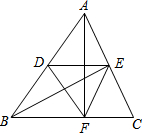 如图,已知在△ABC中,AB=BC=8,AC=6,AF⊥BC于点F,BE⊥AC于点E,取AB的中点D,则△DEF的周长为11.
如图,已知在△ABC中,AB=BC=8,AC=6,AF⊥BC于点F,BE⊥AC于点E,取AB的中点D,则△DEF的周长为11.
分析 根据等腰三角形三线合一的性质可得BE是△ABC的中线,然后根据直角三角形斜边上的中线等于斜边的一半可得DF=$\frac{1}{2}$AB,EF=$\frac{1}{2}$AC,然后判断出DE是△ABC的中位线,根据三角形的中位线平行于第三边并且等于第三边的一半可得DE=$\frac{1}{2}$BC,然后根据三角形的周长公式列式计算即可得解.
解答 解:∵BE⊥AC,
∴BE是△ABC的中线,
∵AF⊥BC,D是AB的中点,
∴DF=$\frac{1}{2}$AB=$\frac{1}{2}$×8=4,EF=$\frac{1}{2}$AC=$\frac{1}{2}$×6=3,
∵BE是△ABC的中线,D是AB的中点,
∴DE是△ABC的中位线,
∴DE=$\frac{1}{2}$BC=$\frac{1}{2}$×8=4,
∴△DEF的周长=4+4+3=11.
故答案为:11.
点评 本题直角三角形斜边上的中线等于斜边的一半的性质,三角形的中位线定理,熟记性质与定理是解题的关键.

练习册系列答案
相关题目
17.下列代数式:a,-ab,m+n,x2+y2,-1,$\frac{1}{2}$ab2c,其中单项式共有( )
| A. | 6个 | B. | 5个 | C. | 4个 | D. | 3个 |
2. 如图,在△ABC中,∠ACB=90°,∠ABC=60°,BD平分∠ABC,P点是BD的中点.若AD=7,则CP的长为( )
如图,在△ABC中,∠ACB=90°,∠ABC=60°,BD平分∠ABC,P点是BD的中点.若AD=7,则CP的长为( )
 如图,在△ABC中,∠ACB=90°,∠ABC=60°,BD平分∠ABC,P点是BD的中点.若AD=7,则CP的长为( )
如图,在△ABC中,∠ACB=90°,∠ABC=60°,BD平分∠ABC,P点是BD的中点.若AD=7,则CP的长为( )| A. | 3 | B. | 3.5 | C. | 4 | D. | 4.5 |
12.函数y=x2+3x-4的图象与y轴的交点坐标是( )
| A. | (2,0) | B. | (-2,0) | C. | (0,4) | D. | (0,-4) |
16.一个长方形的周长为6a+8b,若一边长为2a+b,则它的另一边长为( )
| A. | 4a+5b | B. | a+b | C. | a+3b | D. | a+7b |
 如图是一个数值转换机的示意图,当输入-3时,输出的结果是28.
如图是一个数值转换机的示意图,当输入-3时,输出的结果是28.
 .
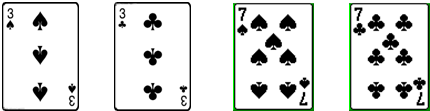
. 表示正,
表示正, .
. 表示负,请你用(1)中的4张牌表示的数写出运算结果为24的算式(写出2个):-[2×(-6)+3×(-4)]=24;[2-3×(-6)]-(-4)=24;;
表示负,请你用(1)中的4张牌表示的数写出运算结果为24的算式(写出2个):-[2×(-6)+3×(-4)]=24;[2-3×(-6)]-(-4)=24;;