题目内容
4.分解因式:(1)(a2+4b2)2-16a2b2;
(2)$\frac{1}{5}$x2y-x4-$\frac{{y}^{2}}{100}$;
(3)(a-b)3-2(b-a)2+(a-b).
分析 (1)原式利用平方差公式及完全平方公式分解即可;
(2)原式提取-1,再利用完全平方公式分解即可;
(3)原式变形后,提取公因式即可得到结果.
解答 解:(1)原式=(a2+4b2+4ab)(a2+4b2-4ab)=(a+2b)2(a-2b)2;
(2)原式=-(x4-$\frac{1}{5}$x2y+$\frac{{y}^{2}}{100}$)=-(x2-$\frac{y}{10}$)2;
(3)原式=(a-b)3-2(a-b)2+(a-b)=(a-b)[(a-b)2-2(a-b)+1]=(a-b)(a-b-1)2.
点评 此题考查了提公因式法与公式法的综合运用,熟练掌握因式分解的方法是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.用四舍五入法得到的近似数3.052万,以下说法正确的是( )
| A. | 它精确到千位 | B. | 它精确到0.001 | C. | 它精确到万位 | D. | 它精确到十位 |
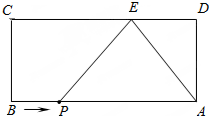 如图,矩形ABCD中,AB=9,AD=4.E为CD边上一点,CE=6.点P从点B出发,以每秒1个单位的速度沿着边BA向终点A运动,连接PE.设点P运动的时间为t秒.
如图,矩形ABCD中,AB=9,AD=4.E为CD边上一点,CE=6.点P从点B出发,以每秒1个单位的速度沿着边BA向终点A运动,连接PE.设点P运动的时间为t秒.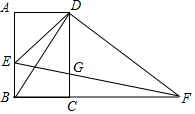 如图,在矩形ABCD中,AB=$\sqrt{3}$,BC=1,点E是AB边上一动点(不与点A,B重合),连接DE,过点D作DF⊥DE交BC的延长线于点F,连接EF交CD于点G,设BE=x.
如图,在矩形ABCD中,AB=$\sqrt{3}$,BC=1,点E是AB边上一动点(不与点A,B重合),连接DE,过点D作DF⊥DE交BC的延长线于点F,连接EF交CD于点G,设BE=x. 如图,已知Rt△ABC中,∠ACB=90°,∠A=30°,AC边上的垂直平分线DE交AB于点D,交AC于E.若DE=3,求AB的长.
如图,已知Rt△ABC中,∠ACB=90°,∠A=30°,AC边上的垂直平分线DE交AB于点D,交AC于E.若DE=3,求AB的长.