题目内容
19.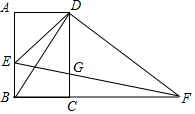 如图,在矩形ABCD中,AB=$\sqrt{3}$,BC=1,点E是AB边上一动点(不与点A,B重合),连接DE,过点D作DF⊥DE交BC的延长线于点F,连接EF交CD于点G,设BE=x.
如图,在矩形ABCD中,AB=$\sqrt{3}$,BC=1,点E是AB边上一动点(不与点A,B重合),连接DE,过点D作DF⊥DE交BC的延长线于点F,连接EF交CD于点G,设BE=x.(1)求证:△AED∽△CFD;
(2)当x为何值时,△BEF的面积最大?
(3)连接BG,若四边形BGDE是平行四边形,求此时x的值.
分析 (1)根据平行四边形的性质得到∠A=∠ADC=∠DCB=90°,根据余角的性质得到∠ADE=∠CDF,由相似三角形的判定定理即可得到结论;
(2)根据相似三角形的性质得到CF=3-$\sqrt{3}$x,根据三角形的面积公式得到函数的解析式,根据二次函数的顶点坐标即可得到结论;
(3)y为最大值时,四边形BGDE是平行四边形,由CG∥BE,得△CFG∽△BFE,得 $\frac{CG}{BE}$=$\frac{CF}{BF}$,求出CG,DG,只要证明BE=DG即可解决问题.
解答 解:(1)在矩形ABCD中,
∵∠A=∠ADC=∠DCB=90°,
∴∠A=∠DCF=90°,
∵DF⊥DE,
∴∠A=∠EDF=90°,
∴∠ADE=∠CDF,
∴△ADE∽△CDF;
(2)∵BE=x,
∴AE=$\sqrt{3}$-x,
∵△ADE∽△CDF,
∴$\frac{AE}{CF}$=$\frac{AD}{CD}$=$\frac{\sqrt{3}}{3}$,
∴CF=3-$\sqrt{3}$x,
∴BF=BC+CF=4-$\sqrt{3}$x,
∴y=$\frac{1}{2}$BE•BF=$\frac{1}{2}$x(4-$\sqrt{3}$x)=-$\frac{\sqrt{3}}{2}$x2+2x,
∵y=-$\frac{\sqrt{3}}{2}$x2+2x=-$\frac{\sqrt{3}}{2}$(x-$\frac{2\sqrt{3}}{3}$)2+$\frac{2\sqrt{3}}{3}$,
∴当x为$\frac{2\sqrt{3}}{3}$ 时,y有最大值;
(3)∵四边形BGDE是平行四边形,
∴BE=DG,
∵CG∥EB,
∴$\frac{CG}{EB}$=$\frac{FC}{FB}$,
∴$\frac{CG}{x}$=$\frac{3-\sqrt{3}x}{4-\sqrt{3}x}$,
∴CG=$\frac{x(3-\sqrt{3}x)}{4-\sqrt{3}x}$,
∴x=$\sqrt{3}$-$\frac{x(3-\sqrt{3}x)}{4-\sqrt{3}x}$,
整理得2$\sqrt{3}$x2-10x+4$\sqrt{3}$=0,
∴($\sqrt{3}$x-2)(2x-2$\sqrt{3}$)=0,
∴x=$\frac{2\sqrt{3}}{3}$或$\sqrt{3}$(舍弃).
∴x=$\frac{2\sqrt{3}}{3}$时,四边形BEDG是平行四边形.
点评 本题考查了相似三角形的判定和性质、求函数的解析式、二次函数的最大值、平行四边形的判定、矩形的性质等知识,熟练掌握相似三角形的判定和性质是解题的关键,学会构建二次函数解决最值问题,学会用方程的思想思考问题,属于中考压轴题.

 名校课堂系列答案
名校课堂系列答案| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
| A. | 第一、二象限 | B. | 第二、四象限 | C. | 第三、四象限 | D. | 第二、三象限 |
| A. | 8 | B. | 9 | C. | 10 | D. | 8或10 |
| A. | 6x2y2=xy•6xy | B. | 2x2-8x-5=2x(x-4)-5 | ||
| C. | x2+3x-4=(x-1)(x+4) | D. | x2+1=x(x+$\frac{1}{x}$) |