题目内容
13. 如图,已知Rt△ABC中,∠ACB=90°,∠A=30°,AC边上的垂直平分线DE交AB于点D,交AC于E.若DE=3,求AB的长.
如图,已知Rt△ABC中,∠ACB=90°,∠A=30°,AC边上的垂直平分线DE交AB于点D,交AC于E.若DE=3,求AB的长.
分析 首先根据线段垂直平分线的性质得到CD=AD,进而求出BD=CD,利用含30度角直角三角形的性质即可求出AB的长.
解答 解:∵AC边上的垂直平分线是DE,
∴CD=AD,DE⊥AC,
∴∠A=∠DCA=30°,
∵∠ACB=90°,
∴∠BCD=∠ACB-∠DCA
=90°-30°=60°,
∵∠B=180°-∠ACB-∠A
=180°-90°-30°
=60°
∴∠BCD=∠B=60°
∴BD=CD,
∴BD=CD=AD=$\frac{1}{2}$AB,
∵DE=3,DE⊥AC,∠A=30°
∴AD=2DE=6,
∴AB=2AD=12.
点评 本题主要考查了含30度角的直角三角形以及线段垂直平分线的性质,解题的关键是求出BD=CD,此题难度不大.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案
相关题目
3.下列各组线段中是成比例线段的是( )
| A. | 1cm,2cm,3cm,4cm | B. | 1cm,2cm,2cm,4cm | ||
| C. | 3cm,5cm,9cm,13cm | D. | 1cm,2cm,2cm,3cm |
1.下列命题中是假命题的是( )
| A. | 一个锐角的补角大于这个角 | |
| B. | 凡能被2整除的数,末位数字必是偶数 | |
| C. | 两条直线被第三条直线所截,同旁内角互补 | |
| D. | 相反数等于它本身的数是0 |
8.已知等腰三角形一边长为2,一边的长为4,则这个等腰三角形的周长为( )
| A. | 8 | B. | 9 | C. | 10 | D. | 8或10 |
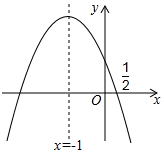 如图,抛物线y=ax2+bx+c的对称轴是x=-1.且过点($\frac{1}{2}$,0),有下列结论:①abc>0;
如图,抛物线y=ax2+bx+c的对称轴是x=-1.且过点($\frac{1}{2}$,0),有下列结论:①abc>0;