Question

15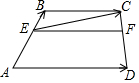．如图，在梯形ABCD中，AD∥BC，AD=3，BC=2，点E、F分别在两腰上，
且EF∥AD，AE：EB=2：1；
（1）求线段EF的长；
（2）设$\overrightarrow{AB}$=$\overrightarrow{a}$，$\overrightarrow{AD}$=$\overrightarrow{b}$，试用$\overrightarrow a$、$\overrightarrow b$表示向量$\overrightarrow{EC}$．

Answer 1

分析 （1）作BM∥CD交AD、EF于M、N两点，将问题转化到△ABM中，利用相似三角形的判定与性质求EN，由EF=EN+NF=EN+AD进行求解；
（2）由$\frac{BC}{AD}$=$\frac{2}{3}$、$\frac{EB}{AB}$=$\frac{1}{3}$得BC=$\frac{2}{3}$AD，EB=$\frac{1}{3}$AB，根据$\overrightarrow{EC}$=$\overrightarrow{EB}+\overrightarrow{BC}$可得答案．

解答 解：（1）作BM∥CD交AD、EF于M、N两点，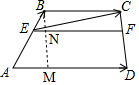

又AD∥BC，EF∥AD，
∴四边形BCFN与MNFD均为平行四边形．
∴BC=NF=MD=2，
∴AM=AD-MD=1．
又$\frac{AE}{EB}$=2，
∴$\frac{BE}{BA}$=$\frac{1}{3}$，
∵EF∥AD，
∴△BEN∽△BAM，
∴$\frac{BE}{BA}=\frac{EN}{AM}$，即$\frac{1}{3}=\frac{EN}{1}$，
∴EN=$\frac{1}{3}$，
则EF=EN+NF=$\frac{7}{3}$；

（2）∵$\frac{BC}{AD}$=$\frac{2}{3}$，$\frac{EB}{AB}$=$\frac{1}{3}$，
∴BC=$\frac{2}{3}$AD，EB=$\frac{1}{3}$AB，
∴$\overrightarrow{EB}$=$\frac{2}{3}$$\overrightarrow{AD}$=$\frac{2}{3}$$\overrightarrow{b}$，$\overrightarrow{EB}$=$\frac{1}{3}$$\overrightarrow{AB}$=$\frac{1}{3}$$\overrightarrow{a}$，
则$\overrightarrow{EC}$=$\overrightarrow{EB}+\overrightarrow{BC}$=$\frac{1}{3}$$\overrightarrow{a}$+$\frac{2}{3}$$\overrightarrow{b}$．

点评 本题主要考查了平行四边形的判定与性质、相似三角形的判定与性质及向量的运算，熟练掌握相似三角形的判定与性质得出对应边的长度之比和向量的基本运算是解题的关键．